Барометрическая формула. Распределение Больцмана

Барометрическая формула выражает закон изменения атмосферного давления при изменении высоты воздушного столба..

Известно, что атмосферное давление с высотой уменьшается. Установим закон изменения атмосферного давления в зависимости от высоты. Упростим задачу, считая температуру постоянной и не изменяющейся с высотой. При возрастании высоты на небольшую величину dx давление уменьшается на малую величину 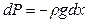, где r - плотность газа, r = m₀n, m₀ - масса молекулы. Удобно выразить плотность газа через макропараметры – температуру и давление. 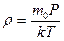Для этого воспользуемся формулой (2.5) и получим , тогда , а .

Разделим переменные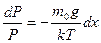

Интегрируя, получаем:

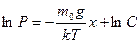, где С - постоянная интегрирования, которую находим из условия : при x=0 и С=Р₀ . Тогда

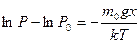или .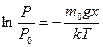

После потенцирования получим барометрическую формулу

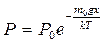. (7-16)

Учитывая, что масса молекулы может быть выражена через молярную массу и число Авогадро 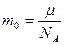, а , показатель экспоненты можно записать через молярную массу и универсальную газовую постоянную:

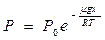(7-16')

Так как при постоянной температуре P ~ n , то можно получить выражение для распределения Больцмана 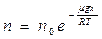или 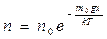. Числитель показателя экспоненты представляет собой потенциальную энергию частицы, находящейся в поле силы тяжести, а знаменатель пропорционален тепловой энергии. Распределение Больцмана справедливо, если частица находится в любом потенциальном поле, поэтому можно обозначить потенциальную энергию частицы через U(х). Тогда распределение Больцмана будет иметь вид

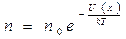(7-17)

Распределение Больцмана – это распределение частиц по потенциальным энергиям. Потенциальная энергия зависит от выбора начала отсчёта, и может быть выражена как U(x) = U₀ + DU(x). Здесь U₀ – потенциальная энергия частиц в начале отсчёта, U(x)- потенциальная энергия в положении x, DU(x)- изменение потенциальной энергии или рассматриваемый интервал потенциальных энергий. Число частиц, потенциальные энергии которых лежат в малом интервале DU(x) от U₀ до U(x) , согласно (3.16), равно:

.

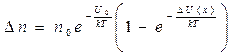Число частиц, потенциальные энергии которых лежат в малом интервале DU(x) вблизи U(x) , равно: .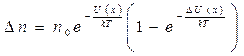

Доля частиц, потенциальные энергии которых лежат в малом интервале DU(x) вблизи U(x) , определяется выражением: 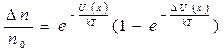. Отсюда видно, что доля частиц 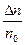, потенциальная энергия которых лежит в заданном интервале DU с ростом U уменьшается, а с ростом интервала DU вблизи некоторого значения энергии U увеличивается.

При большом числе частиц n₀ и бесконечно малом интервале энергий dU доля частиц 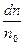, потенциальная энергия которых лежит в в интервале dU вблизи потенциальной энергии U, имеет смысл вероятности того, что любая частица может иметь потенциальную энергию в указанном интервале вблизи заданного значения потенциальной энергии.

Таким образом, барометрическая формула и распределение Больцмана по потенциальным энергиям имеет вид распределения Гаусса.