Среднее число столкновений и среднее время свободного пробега молекул

Определим среднее число столкновений молекулы газа за одну секунду. Положим, что молекулы-мишени равномерно распределены по объёму с концентрацией n. Пусть все молекулы, кроме одной, покоятся. Тогда движущаяся молекула за одну секунду пройдёт расстояние, численно равное средней скорости 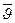, и столкнётся со всеми молекулами, которые окажутся на её пути. Это будут те молекулы, центры которых расположены в объёме цилиндра, длиной 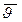и площадью основания σ (рис.8.3).Объём этого цилиндра равен 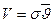, а число молекул в нём равно 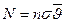. Таким же будет число столкновений, которое испытывает молекула. Если учесть, что движутся все молекулы в выделенном объёме, то при подсчёте числа столкновений нужно учитывать не абсолютную скорость (относительно стенок сосуда), а относительную скорость молекулы, то есть скорость относительно тех молекул, с которыми она сталкивается. Определим относительную скорость двух молекул, движущихся со скоростями 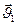и : . 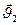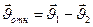Возведём в квадрат обе части последнего равенства и получим:

.

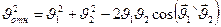Усредним это уравнение и получим: 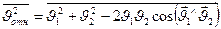. Учтём, что 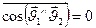, а 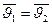, получим .

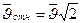Учитывая это, среднее число столкновений молекулы за одну секунду равно:

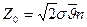(8-4)

С учётом формулы (8-1) получим:

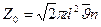(8-5)

В системе интернациональной единица измерения Z₀ равна с ^{- 1}.

Среднее число столкновений за секунду, испытываемое всеми N молекулами определяют с учётом того, что в столкновениях участвуют пары молекул, а вероятностью столкновения трёх и более молекул пренебрегают:

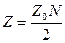(8-6)

Среднее число столкновений молекул за времяt:

(8-7)

Зная среднее число столкновений одной молекулы за секунду Z₀ , можно найти время между двумя последовательными соударениями молекулы – время свободного пробега :

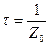(8-8)