Средняя длина свободного пробега молекул

Расстояние, которое молекула проходит между двумя последовательными столкновениями, называется длиной свободного пробега. Так как молекул много, их движения беспорядочны и столкновения случайны, то длины свободного пробега на зигзагообразном пути молекулы могут быть разными. Поэтому целесообразно говорить о средней длине свободного пробега 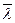. Величины сечения рассеяния и концентрации молекул не зависят от пути, пройденного частицей, поэтому вероятность столкновения растёт пропорционально проходимому частицей пути. Длина пути 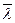, при которой вероятность столкновения равна единице, называется средней длиной свободного пробега. Для математической записи 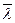используем формулу (8-2), заменив dx на 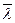и приравняв вероятность столкновения единице, получим:

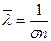(8-9)

Средняя длина свободного пробега может быть выражена через среднюю скорость молекул и среднее время свободного пробега, учитывая то, что молекулы идеального газа движутся равномерно и прямолинейно между двумя последовательными соударениями:

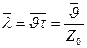(8-10)

Учитывая формулу (8-5), получим:

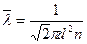(8-11)

Среднюю длину свободного пробега можно выразить через параметры состояния газа – давление и температуру, учитывая, что 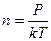, получим:

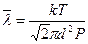(8-12)

Средняя длина свободного пробега при фиксированной температуре обратно пропорциональна давлению, а при фиксированном давлении – прямо пропорциональна температуре.