Влияние растворителя на электронные спектры поглощения сложных молекул.
Пусть в газовой фазе молекула имеет Гамильтониан Ĥ0 , уровни энергии E0j , волновые функции ψ0j . По этим характеристикам и внешнему полю Ē мы можем определить такие величины как дипольный момент μ0j , поляризуемость ά0j , энергии переходов ΔE0j и другие.
При помещении молекулы в конденсированную фазу произойдут следующие изменения. Во-первых, изменится гамильтониан за счет взаимодействия с окружающей средой: Ĥ0→Ĥ0+Vвз=Ĥ1 . Это приведет к новым значениям уровней энергии Ej , волновым функциям ψj , дипольным моментам μj и т.д. Во-вторых, в среде изменится электрическое поле, действующее на молекулу: Ē→Ēэфф . Обсудим сначала учет члена Vвз в гамильтониане. Все молекулярные взаимодействия можно разделить на два класса: специфические (Н-связи, комплексы с переносом заряда, валентные взаимодействия и т.д.), зависящие от локального окружения молекулы, и универсальные, которые существуют во всех системах кроме идеального газа (взаимодействий Ван дер Ваальса). Расчет специфических взаимодействий является предметом квантовой химии. Универсальные взаимодействия связаны с наличием у молекул дипольных моментов различной природы и классифицируются согласно происхождению этих дипольных моментов.
Ориентационная составляющая взаимодействий Ван дер Ваальса определяется ориентацией постоянных дипольных моментов молекул и дает следующую формулу для энергии парного взаимодействия двух молекул как функция расстояния:
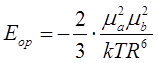 (4.1)
(4.1)
Индукционная составляющая определяется взаимодействием диполей, индуцированных постоянными диполями соседних молекул, и имеет следующую энергию:
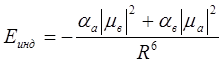 (4.2)
(4.2)
Дисперсионная составляющая определяется взаимодействием переменных диполей, возникающих в молекулах под влиянием мгновенных переменных диполей соседей. Энергия может быть выражена через потенциалы ионизации I и поляризуемости α соответствующих молекул:
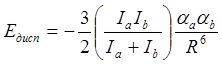 (4.3)
(4.3)
Измененное электрическое поле в среде определяется с помощью теории Онзагера по следующим формулам:
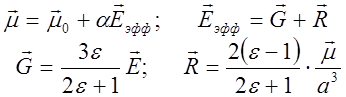 (4.4)
(4.4)
В этих формулах 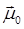 — постоянный дипольный момент молекулы,
— постоянный дипольный момент молекулы, 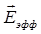 — эффективное, локальное поле в среде, действующее на молекулу,
— эффективное, локальное поле в среде, действующее на молекулу, 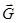 и
и 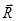 — так называемые активное и реактивное поля Онзагера, а — радиус полости Онзагера, ε — диэлектрическая проницаемость.
— так называемые активное и реактивное поля Онзагера, а — радиус полости Онзагера, ε — диэлектрическая проницаемость.
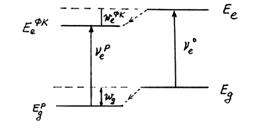 |
При учете этих факторы картина энергетических уровней молекулы при помещении из газовой фазы в раствор изменяется так как показано на схеме:
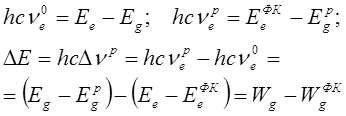 (4.5)
(4.5)
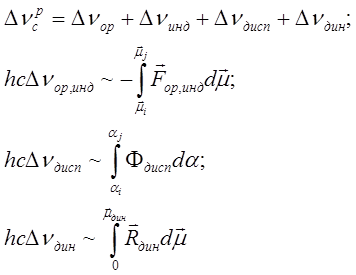 (4.6)
(4.6)
В этих выражениях 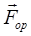 — сила, соответствующая энергии ориентационного взаимодействия,
— сила, соответствующая энергии ориентационного взаимодействия, 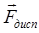 —энергия парного дисперсионного взаимодействия,
—энергия парного дисперсионного взаимодействия, 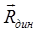 — составляющая реактивного поля, индуцируемая световой волной. Соответствующие сдвиги частот определяются работой сил, определяющихся соответствующими энергиями взаимодействия, при изменении дипольного момента или поляризуемости от μi , αi в состоянии i до μi , αi в состоянии j. Эти соображения приводят к следующему выражению для сдвига спектра поглощения молекулы при помещении в раствор.
— составляющая реактивного поля, индуцируемая световой волной. Соответствующие сдвиги частот определяются работой сил, определяющихся соответствующими энергиями взаимодействия, при изменении дипольного момента или поляризуемости от μi , αi в состоянии i до μi , αi в состоянии j. Эти соображения приводят к следующему выражению для сдвига спектра поглощения молекулы при помещении в раствор.
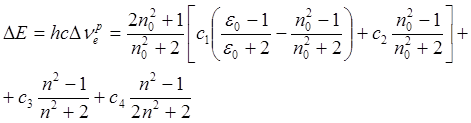 (4.9)
(4.9)
В этой формуле использованы следующие обозначения.
n0 — показатель преломления растворителя при больших длинах волн (ИК-область)
n — показатель преломления растворителя в области исследуемой полосы.
ε0 — статическая диэлектрическая проницаемость растворителя
 (ориентационный член), а — радиус полости Онзагера
(ориентационный член), а — радиус полости Онзагера
(индукционные взаимодействия)
(дисперсионные взаимодействия)
I — потенциал ионизации растворенного вещества,
I΄ — потенциал ионизации растворителя.
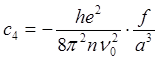 - (динамический эффект)
- (динамический эффект)
f - сила осциллятора перехода в газе.
Поскольку в газе n=1, а в растворе n>1, последний член в формуле (4.9), содержащий С4 всегда отрицателен, и поэтому он вызывает красный сдвиг спектра поглощения при растворении. Действие других членов этой формулы зависит от соотношения между μg, αg и μe, αe — дипольным моментом и поляризуемостью в основном и возбужденном состояниях соответственно.
Дата добавления: 2015-06-10; просмотров: 1940;
