Амплитудный и фазовый спектры периодической функции

Пусть f(x) удовлетворяет условиям теоремы Дирихле на [-l;l], и периодична периода 2l, тогда она представима рядом Фурье в комплексной форме

где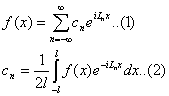

с комплексной амплитудой и волновым числом 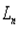. Тем самым мы представляем f(x) в виде суммы бесконечного множества комплексных гармонических колебаний,

частоты 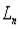которых образуют бесконечную арифметическую прогрессию с разностью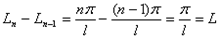

Амплитуды и фазы гармонических колебаний, отвечающих комплексной гармонике 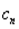, определяются формулами

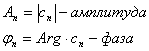
Так как аргумент комплексного числа есть функция многозначная, то для вычисления фаз 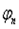нужно предварительно договариваться о выборе значений 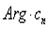. Можно, например, условиться брать главное значение аргумента, т.е. значение, удовлетворяющее условию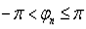

Амплитуды 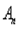и фазы 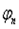гармонических колебаний, в виде суммы которых представляется периодическая функция f(x), играют большую роль в различных прикладных вопросах. Для наглядного представления этих амплитуд и фаз делают следующие построения: возьмем ось частот 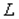и на этой оси отложим частоты .

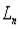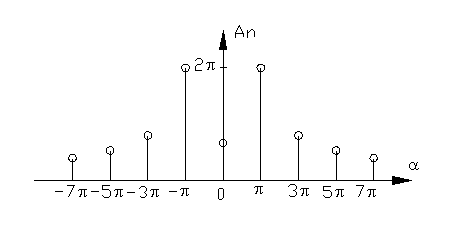
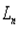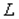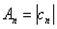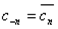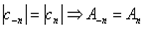Против каждой частоты перпендикулярно к оси будем откладывать соответствующую амплитуду .Так как , то , т.е. амплитудный спектр симметричен относительно прямой L=0, а так как 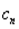→0 при n→∞, то ординаты амплитудного спектра стремятся к нулю по мере удаления от прямой L=0, причем порядок убывания этих ординат не ниже чем 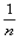(без доказательства).

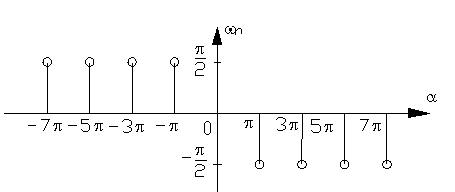
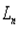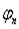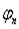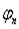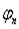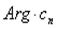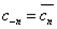Аналогично строится фазовый спектр функции f(x).Для этого против точек оси частот откладываются отрезки длины (вверх >0 и вниз <0).Так как = и , то 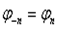, т.е. фазовый спектр симметричен относительно точки L=0.

Пример. В условиях предыдущего примера построить амплитудный и фазовый спектры.

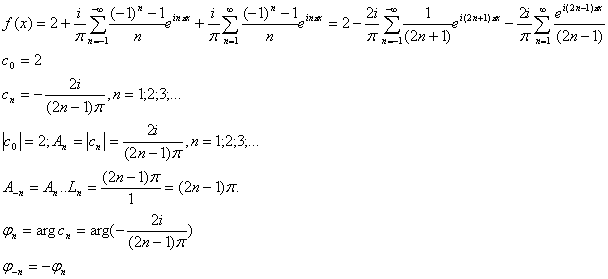
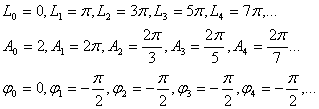
Большое значение при разработке различных летательных аппаратов их двигателей, влияние, распространяемого тепла по поверхности аппаратов и по всей их плоскости имеют исследования Фурье в области теплопроводности.