Комплексная форма тригонометрического ряда Фурье
Жан Фурье родился 21 марта 1768 года. Его первые труды относятся к алгебре. В лекциях 1796 года он изложил теорему о числе действительных корней алгебраического уравнения, лежащих между данными границами (опубликовано в 1820 году), названную его именем; полное решение вопроса о числе действительных корней алгебраического уравнения было получено в 1829 году Ж. Ш. Ф. Штурмом.
В 1818 году Фурье исследовал вопрос об условиях применимости разработанного Исааком Ньютоном метода численного решения уравнений, не зная об аналогичных результатах, полученных в 1768 году французским математиком Ж. Р. Мурайлем. Итогом работ Фурье по численным методам решения уравнений является "Анализ определённых уравнений", изданный посмертно в 1831 году.
Основной областью занятий Жана Фурье была математическая физика. В 1807 и 1811 годах он представил Парижской АН свои первые открытия по теории распространения тепла в твёрдом теле, а в 1822 году опубликовал работу "Аналитическая теория тепла", сыгравшую большую роль в последующей истории математики. В ней Фурье вывел дифференциальное уравнение теплопроводности и развил идеи, в самых общих чертах намеченные ранее Даниилом Бернулли, разработал для решения уравнения теплопроводности при тех или иных заданных граничных условиях метод разделения переменных (Фурье метод), который он применял к ряду частных случаев (куб, цилиндр и др.). В основе этого метода лежит представление функций тригонометрическими рядами Фурье, которые хотя и рассматривались иногда ранее, но стали действенным и важным орудием математической физики только у Фурье. Метод разделения переменных получил дальнейшее развитие в трудах С. Пуассона, Михаила Васильевича Остроградского и других математиков 19 века.
"Аналитическая теория тепла" явилась отправным пунктом создания теории тригонометрических рядов и разработки некоторых общих проблем математического анализа. Фурье привёл первые примеры разложения в тригонометрические ряды Фурье функций, которые заданы на различных участках различными аналитическими выражениями. Тем самым он внёс важный вклад в решение знаменитого спора о понятии функции, в котором участвовали крупнейшие математики 18 века. Его попытка доказать возможность разложения в тригонометрический ряд Фурье любой произвольной функции была неудачна, но положила начало большому циклу исследований, посвященных проблеме представимости функций тригонометрическими рядами (П. Дирихле,Николай Иванович Лобачевский, Б. Риман и др.). С этими исследованиями было в значительной мере связано возникновение теории множеств и теории функций действительного переменного.
Ряды Фурье для комплексных функций
Рассмотрим элементы теории рядов Фурье для комплексных функций, т.е. функций вида 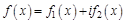 , где i – мнимая единица,
, где i – мнимая единица, 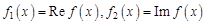 – вещественные функции вещественного аргумента. Обозначим символом
– вещественные функции вещественного аргумента. Обозначим символом 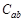 множество комплексных кусочно-непрерывных функций, определенных на промежутке
множество комплексных кусочно-непрерывных функций, определенных на промежутке 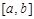 .
.
Скалярным произведением функций 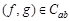 назовем комплексное число
назовем комплексное число
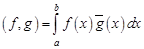 ,
,
где 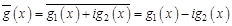 – функция, комплексно сопряженная с функцией
– функция, комплексно сопряженная с функцией 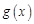 .свойства скалярного произведения комплексных функцийследующие:
.свойства скалярного произведения комплексных функцийследующие:
1. 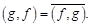
2. билинейность
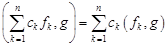 ,
, 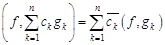 .
.
Как и ранее, функции f и g будем называть ортогональными, если их скалярное произведение равно нулю.
Определение нормы функции оставим прежним, так что
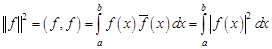 .
.
Свойства нормы, претерпевшие изменения при переходе от вещественных функций к комплексным, следующие:
1. теорема косинусов. 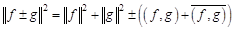
или в более общем виде
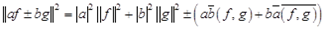 . (1.2)
. (1.2)
2. Обобщенная теорема Пифагора.Если 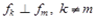 , то
, то
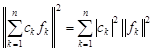 .
.
3. Неравенство Коши – Буняковского.Если функции 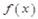 и
и 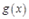 непрерывны, то
непрерывны, то 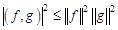 .
.
В самом деле, если 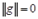 , то
, то 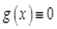 на
на 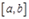 , и доказываемое неравенство выполняется. Пусть
, и доказываемое неравенство выполняется. Пусть 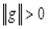 . Число
. Число 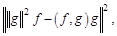 очевидно, не отрицательно. С другой стороны, по формуле (1.2), где
очевидно, не отрицательно. С другой стороны, по формуле (1.2), где 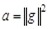 и
и 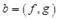 , имеем
, имеем
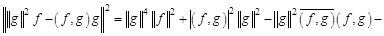
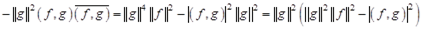 .
.
Таким образом, 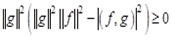 , а так как
, а так как 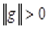 , то
, то  , что и требовалось доказать.
, что и требовалось доказать.
Пусть теперь система комплексных функций
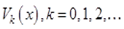 (1.3)
(1.3)
ортогональна на промежутке 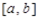 . Сопоставим функции
. Сопоставим функции 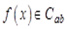 ее ряд Фурье
ее ряд Фурье
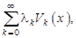 (1.4)
(1.4)
где коэффициенты Фурье
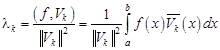 .
.
Введем обозначения: 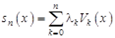 – частичная сумма ряда Фурье;
– частичная сумма ряда Фурье; 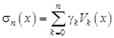 – произвольная линейная комбинация функций
– произвольная линейная комбинация функций 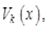 где
где 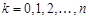 .
.
Тогда, так же, как для вещественных функций выполняется неравенство
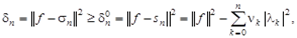 (1.5)
(1.5)
где 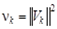 , причем равенство имеет место тогда и только тогда, когда
, причем равенство имеет место тогда и только тогда, когда 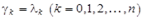 , т.е. среди всех функций
, т.е. среди всех функций 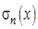 функция
функция 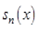 дает наилучшее среднеквадратическое приближение к функции
дает наилучшее среднеквадратическое приближение к функции 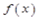 .
.
Сходимость ряда в среднем и замкнутость системы функций определяются
а) если для некоторой функции 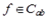 выполняется равенство Парсеваля
выполняется равенство Парсеваля
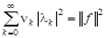 , (1.6)
, (1.6)
то ряд (1.4) сходится в среднем к 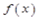 , т.е.
, т.е. 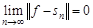 ;
;
б) ортогональная система функций (1.3) называется замкнутой на промежутке 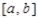 , если равенство Парсеваля выполняется для каждой функции из
, если равенство Парсеваля выполняется для каждой функции из 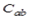 .
.
Введем в рассмотрение систему комплексных функций
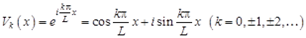 . (1.7)
. (1.7)
Свойства системы функции(1.7) следующие:
1. 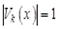 .
.
2. Функции 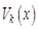 являются 2L -периодичными:
являются 2L -периодичными: 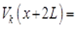
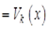 .
.
3. Система функций (1.7) ортогональна на промежутке [–L , L ]. Действительно, при 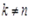
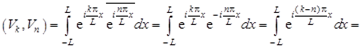
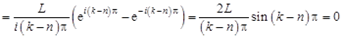 .
.
Здесь использована формула 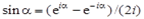 .
.
4. 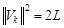 .
.
Ряд Фурье для функции 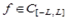 по системе функций (1.7) имеет вид
по системе функций (1.7) имеет вид
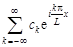 , (1.8)
, (1.8)
где коэффициенты Фурье
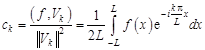 . (1.9)
. (1.9)
Система функций (1.7) замкнута на [–L , L ] , поэтому для нее справедливы следующие утверждения:
а) ряд (1.8) сходится в среднем к 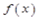 ,
,
б) для любой функции из 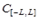 выполняется равенство Парсеваля
выполняется равенство Парсеваля 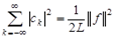 ,
,
в) среднеквадратическая погрешность, возникающая при замене функции 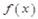 частичной суммой
частичной суммой 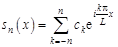 ее ряда Фурье,
ее ряда Фурье,
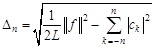 .
.
Теорема Дирихле. Если вещественная и мнимая части функции 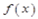 удовлетворяют на промежутке [–L , L ] условиям Дирихле, то функция
удовлетворяют на промежутке [–L , L ] условиям Дирихле, то функция 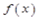 является суммой своего ряда Фурье:
является суммой своего ряда Фурье:
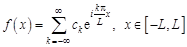 . (1.10)
. (1.10)
Комплексная форма тригонометрического ряда Фурье
Пусть вещественная функция 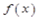 удовлетворяет условиям Дирихле на промежутке [–L , L ]. Запишем ее разложение в тригонометрический ряд Фурье:
удовлетворяет условиям Дирихле на промежутке [–L , L ]. Запишем ее разложение в тригонометрический ряд Фурье:
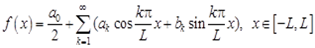 , (2.1)
, (2.1)
где
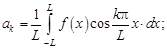
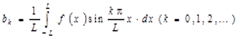 . (2.2)
. (2.2)
Если в (2.1) выразить 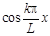 и
и 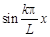 через показательную функцию от мнимого аргумента:
через показательную функцию от мнимого аргумента:
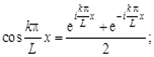
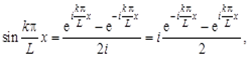
то получим ряд
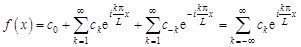 , (2.3)
, (2.3)
где в силу (2.2)
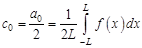 ;
;
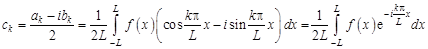 ;
;
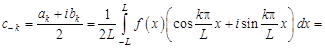
= 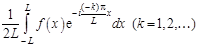
Последние три формулы можно объединить:
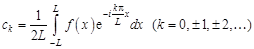 . (2.4)
. (2.4)
Ряд (2.3) с коэффициентами (2.4) называется тригонометрическим рядом Фурье в комплексной форме.
Пример 1. Разложить функцию 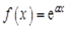 , где
, где 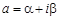 – комплексное число, в ряд Фурье на промежутке
– комплексное число, в ряд Фурье на промежутке 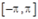 .
.
Решение. Найдем коэффициенты Фурье:
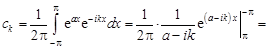
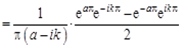 .
.
Поскольку 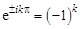 , то
, то
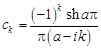 ,
, 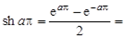
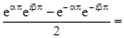
= 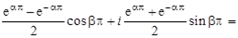
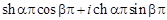 .
.
Искомое разложение будет иметь вид
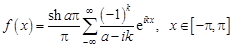 , (2.5)
, (2.5)
где учтено, что
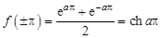 .
.
Применяя к ряду (2.5) равенство Парсеваля
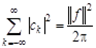 , (2.6)
, (2.6)
можно найти сумму еще одного числового ряда. Действительно, в нашем случае
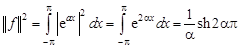 ;
;
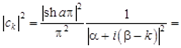
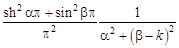 .
.
Тогда из (2.6) следует
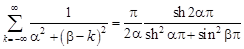 .
.
Принята, особенно в электротехнике и радиотехнике, следующая терминология. Выражения 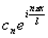 называют гармоникой, иногда так же называют комплексной гармоникой,
называют гармоникой, иногда так же называют комплексной гармоникой, 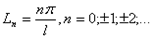 называют волновыми числами. Совокупность волновых чисел называется спектром. Если обкладывать эти числа на числовой оси, то получим совокупность отдельных точек. Такую совокупность называют дискретной, а соответствующий спектр дискретным.
называют волновыми числами. Совокупность волновых чисел называется спектром. Если обкладывать эти числа на числовой оси, то получим совокупность отдельных точек. Такую совокупность называют дискретной, а соответствующий спектр дискретным.
Ряды Фурье применяются при разработке радиоэлектронных систем управления и наведения различных зенитно-ракетных комплексов, космических аппаратов, при расчетах заданных параметров управления полетом.
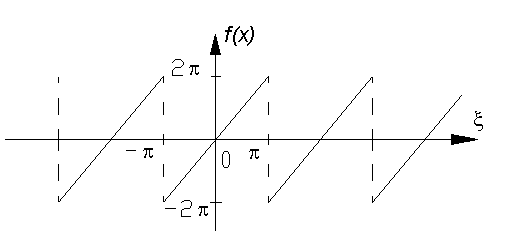
Пример 4. Представить рядом Фурье в комплексной форме функцию
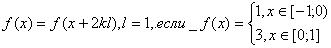
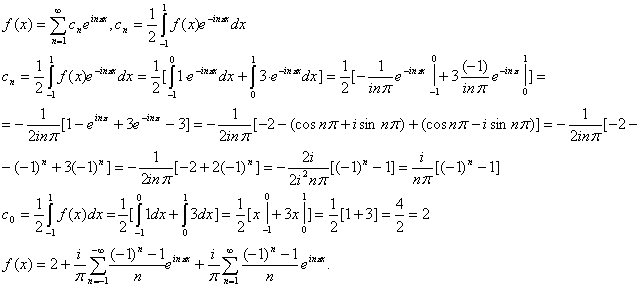
Дата добавления: 2015-06-10; просмотров: 3772;
