Фундаментальное решение уравнения теплопроводности.

Преобразуем формулу 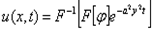к более удобному ”явному” виду. Для этого запишем ее в интегралах

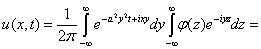
меняем порядок интегрирования

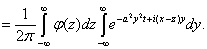(4.1)

В формуле (4.1) внутренний интеграл есть преобразование Фурье от функции 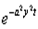при значении аргумента –(x-z), поэтому имеем

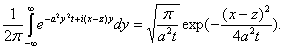
Подставляя это в (4.1), получим

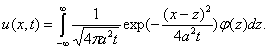(4.2)

Функцию

называют фундаментальным решением уравнения теплопроводности

В заключение хотелось бы отметить, что о Фурье мы прежде всего вспоминаем как об авторе “Аналитической теории теплоты” (1822 г.). В силу общности метода эта книга стала источником всех современных методов математической физики, относящихся к интегрированию уравнений в частных производных при заданных граничных условиях.