А) Уравнения, описывающие переходные процессы.
Из уравнения механической характеристики (5.4) получим:
М = ½b½w0 - ½b½w. (5.5,а)
Подставив (5.5,а) в уравнение движения (5.1), после элементарных преобразований будем иметь:
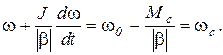(5.13)
Коэффициент при производной 
как и раньше, - электромеханическая постоянная времени Тм. Правая часть уравнения представляет собою скорость wс, соответствующую моменту сопротивления Мс, однако, в рассматриваемом случае w0 , а значит и wс не постоянные величины, а известные функции времени w0(t) и wc(t). Таким образом, уравнение (5.13) имеет вид:
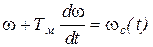. (5.14)
Решение этого дифференциального уравнения определит искомую зависимость w(t).
Для получения зависимости М(t) удобно воспользоваться непосредственно уравнением движения (5.1), подставив в него производную найденной функции w(t):
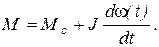(5.15)
Правая часть уравнения (5.14), вообще говоря, может иметь любой вид. Закон w0(t) в случае безынерционного преобразователя формируется на его входе; при инерционном преобразователе закон w0(t) связан со свойствами преобразователя. В ряде случаев закон w0(t) формируется таким образом, чтобы получить требуемый закон w(t).
б) Уравнение переходных процессов при линейном законе wс(t)
Получим решение уравнения (5.14) для одного важного вида функции wс(t) - для линейного изменения wс во времени:
wс(t) = а + kt. (5.16)
Такой закон может быть сформирован при безынерционном преобразователе с помощью задатчика интенсивности.
Мы используем здесь общее уравнение прямой, не накладывая пока никаких ограничений на величины а и k с тем, чтобы, рассматривая частные случаи, можно было пользоваться полученным общим результатом.
Уравнение (5.14) с учетом (5.16) имеем вид:
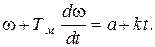(5.17)
Решение будем искать, как и прежде, в виде суммы свободной wсв и принужденной wпр составляющих:
w = wсв + wпр . (*)
Свободная составляющая, то есть решение однородного уравнения, полученного из (5.17) имеет вид:
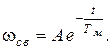
Принужденную составляющую будем искать, учитывая (5.16), в виде:
wпр = В + kt,
так как в установившемся режиме скорость будет линейно изменяться во времени. Подставив wпр в (5.17) получим:
В + kt + kTм = a + kt
или
B = a - kT м.
Подставим теперь wсв иwпр в (*):
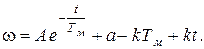
Постоянную А найдем, используя начальные условия: при t = 0 w = wнач:
wнач = А + а - kTм,
откуда
А = wнач - а + kTм
Окончательно будем иметь:
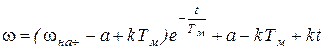. (5.18)
Перейдем теперь к рассмотрению некоторых конкретных переходных процессов в системе П-Д.
Дата добавления: 2015-05-19; просмотров: 2076;