M Решение.

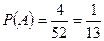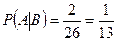, , следовательно, события независимы;

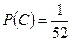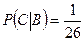, , следовательно, события зависимы;

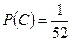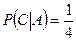, , следовательно, события зависимы. l

Определение. События 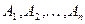независимы в совокупности, если для всех

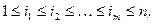
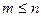, выполнено равенство

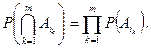
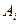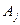
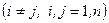Замечание. Из попарной независимости событий и не следует, что события 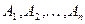независимы в совокупности.

Пример 10. Пусть эксперимент состоит в выборе одного из четырех шаров. Пусть три из них занумерованы цифрами 1, 2, 3, а на четвертом шаре имеются все эти цифры. Обозначим через 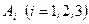событие, состоящее в том, что на выбранном шаре имеется цифра 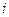. Зависимы ли события 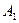, 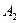и .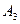

m Решение. Так как, каждая цифра встречается дважды, то

.

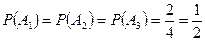Так как две различные цифры присутствуют только на одном шаре, то

,

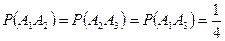следовательно, события 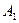, 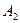и 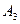попарно независимы.

Все три различные цифры присутствуют только на одном шаре

.

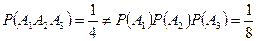Таким образом, получаем, что события 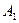, 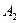и 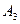зависимы в совокупности, в то время как они являются попарно независимыми. l