Независимость событий
Определение. События A и B называются независимыми, если условная вероятность события A при условии B совпадает с безусловной вероятностью события A, т.е.
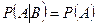 . (3.3.1)
. (3.3.1)
Можно сформулировать и другое определение независимых событий  и
и 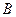 .
.
Определение. События A и B независимы, если
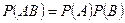 . (3.3.2)
. (3.3.2)
Очевидно, что данные два определения равносильны.
Пример 7. Пусть события  и
и 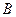 независимы. Доказать, что независимыми являются пары событий
независимы. Доказать, что независимыми являются пары событий 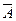 и
и 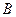 ,
,  и
и 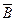 ,
, 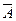 и
и 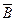 .
.
m Решение. Применяя определение независимости событий, и используя вероятность противоположного события, имеем
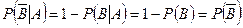 , т.е.
, т.е. 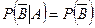 ;
;
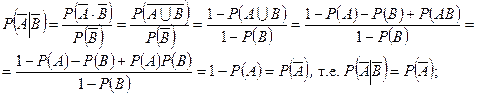
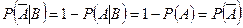 , т.е.
, т.е. 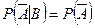 . l
. l
Пример 8. Зависимы или независимы несовместные события.
m Решение. Пусть события  и
и 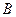 несовместные, т.е.
несовместные, т.е. 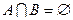 , причем
, причем 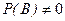 . Тогда
. Тогда 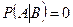 , т.к. события не пересекаются. Следовательно
, т.к. события не пересекаются. Следовательно  и
и 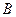 зависимы.
зависимы.
Таким образом, несовместные события зависимы. l
Пример 9. Из полной колоды карт (52 листа) вынимается одна карта. Рассматриваются следующие события:
 — появление туза;
— появление туза;
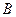 — появление карты красной масти;
— появление карты красной масти;
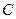 — появление бубнового туза.
— появление бубнового туза.
Зависимы или независимы следующие пары событий: 1)  и
и 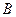 , 2)
, 2) 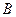 и
и 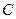 , 3)
, 3)  и
и 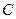 ?
?
Дата добавления: 2015-05-28; просмотров: 887;
