Формула полной вероятности
Определение. События 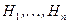 образуют полную группу несовместных событий (являются гипотезами),если они удовлетворяют двум требованиям:
образуют полную группу несовместных событий (являются гипотезами),если они удовлетворяют двум требованиям:
§ они попарно несовместны, т.е. 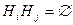 при
при 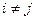 ;
;
§ в результате опыта одно из событий обязательно должно произойти, т.е. 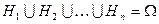 .
.
Пусть имеется некоторое событие  и известны вероятности
и известны вероятности 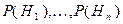 и условные вероятности
и условные вероятности 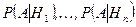 . Найдем вероятность
. Найдем вероятность 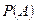 .
.
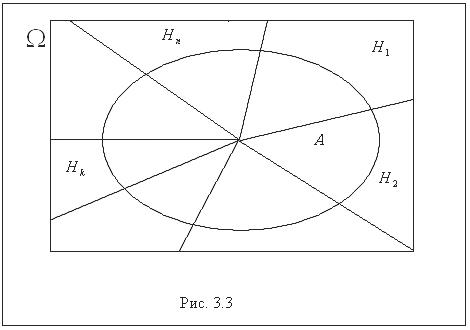
Событие  можно представить в виде (рис. 3.3):
можно представить в виде (рис. 3.3):
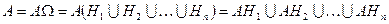 ,
,
причем события 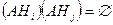 при
при 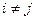 , т.е. события
, т.е. события 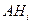 и
и 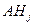 несовместны.
несовместны.
Тогда по аксиоме сложения:
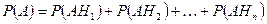 .
.
Далее, применяя теорему умножения вероятностей 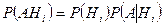 , получаем:
, получаем:
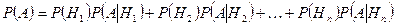 . (3.4.1)
. (3.4.1)
Это и есть формула полной вероятности.
Пример 11. Имеются две урны: в первой 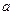 белых и
белых и 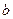 черных шаров; во второй
черных шаров; во второй 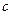 белых и
белых и 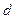 черных шаров. Из первой урны во вторую наудачу перекладывают один шар. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.
черных шаров. Из первой урны во вторую наудачу перекладывают один шар. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.
m Решение. Пусть искомое событие  — вынут белый шар. Рассмотрим следующие гипотезы:
— вынут белый шар. Рассмотрим следующие гипотезы:
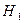 — переложен белый шар;
— переложен белый шар;
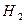 — переложен черный шар.
— переложен черный шар.
Очевидно, что
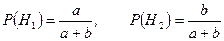 ;
;
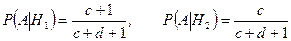 .
.
Теперь по формуле полной вероятности (3.4.1) получаем:
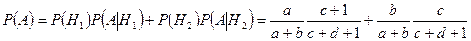 . l
. l
Пример 12. В условиях предыдущей задачи из первой урны перекладывают сразу три шара (предполагается, что 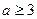 и
и 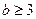 ). Найти вероятность того, что шар, взятый из второй урны, будет белым.
). Найти вероятность того, что шар, взятый из второй урны, будет белым.
m Решение. Пусть искомое событие  — вынут белый шар. Рассмотрим гипотезы:
— вынут белый шар. Рассмотрим гипотезы:
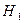 — вынутый шар принадлежит 1-ой урне;
— вынутый шар принадлежит 1-ой урне;
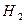 — вынутый шар принадлежит 2-ой урне.
— вынутый шар принадлежит 2-ой урне.
Так как во второй урне 3 шара принадлежат 1-ой урне, а 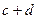 принадлежат 2-ой, то вероятности гипотез равны:
принадлежат 2-ой, то вероятности гипотез равны:
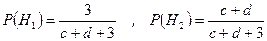 .
.
Вероятность появления белого шара из первой урны не зависит от того, вынимается ли этот шар непосредственно из первой урны или после перекладывания во вторую. Следовательно, условная вероятность появления белого шара при условии того, что он изначально находился в первой урне, равна:
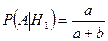 .
.
Аналогично условная вероятность появления белого шара при условии того, что он изначально находился во второй урне, равна:
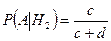 .
.
По формуле полной вероятности (3.4.1) получаем:
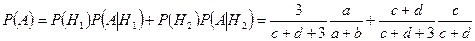 . l
. l
Пример 13. Среди 30 экзаменационных билетов: 25 «хороших» и 5 «плохих». Какова вероятность, отвечая вторым, взять «хороший» билет?
m Решение. Пусть искомое событие  — второй отвечающий взял «хороший» билет. Рассмотрим следующие гипотезы:
— второй отвечающий взял «хороший» билет. Рассмотрим следующие гипотезы:
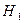 — первый отвечающий взял «хороший» билет;
— первый отвечающий взял «хороший» билет;
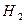 — первый отвечающий взял «плохой» билет.
— первый отвечающий взял «плохой» билет.
Очевидно, что
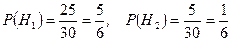 ;
;
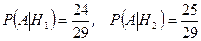 .
.
По формуле полной вероятности (3.4.1), получим:
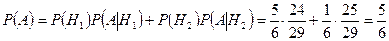 . l
. l
Дата добавления: 2015-05-28; просмотров: 2887;
