Формула Байеса

Пусть имеется полная группа несовместных событий 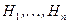. Требуется найти вероятность события 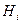, если известно, что событие произошло.

По определению условной вероятности (3.4.1), имеем:

.

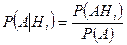Далее, применяя теорему умножения вероятностей 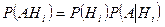, получаем

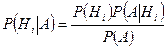. (3.5.1)

Последняя формула называется формулой Байеса или формулой гипотез (события 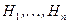называют еще гипотезами).

Если после опыта, который заканчивается появлением события , производится еще один опыт, в котором появляется или не появляется событие 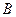, то условная вероятность этого последнего события вычисляется по формуле полной вероятности, в которую подставлены не прежние вероятности гипотез 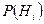, а новые :

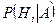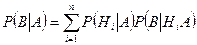. (3.5.2)

Пример 14. Имеются три урны: в первой — белых и черных шаров; во второй — 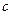белых и 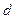черных шаров, в третьей — 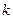белых шаров. Выбирается наугад урна и из нее вынимается шар. Этот шар оказался белым. Найти вероятность того, что этот шар вынут из первой, второй или третьей урны.

m Решение. Пусть искомое событие — вынутый шар белый. Рассмотрим следующие гипотезы:

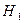— выбрана первая урна;

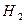— выбрана вторая урна;

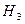— выбрана третья урна.

Очевидно, что:

.

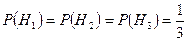Условные вероятности равны:

.

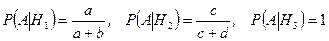По формуле полной вероятности (3.4.1), находим, что

.

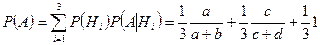По формуле Байеса (3.5.1), находим:

.

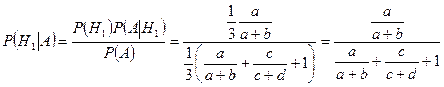Аналогично получаем, что

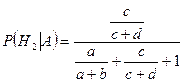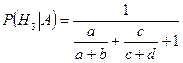, . l

Пример 15. Имеются две урны: в первой — 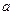белых и 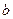черных шаров; во второй — 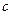белых и 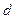черных шаров. Выбирается наугад одна из урн и из нее вынимается один шар. Этот шар оказался белым (событие А). найти вероятность того, что следующий шар, который мы вынимаем из той же урны, будет тоже белым(событие В).

m Решение. Рассмотрим следующие гипотезы:

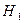— выбрана первая урна;

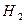— выбрана вторая урна.

Очевидно, что вероятности выбора урн равны:

.

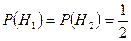Находим условные вероятности:

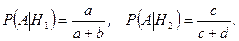
По формуле полной вероятности (3.4.1), получаем:

.

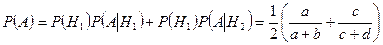По формуле Байеса (3.5.1), получаем:

.

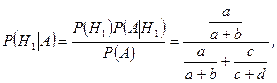
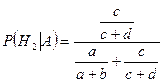Далее применяем (3.5.2):

.

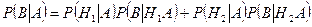Условная вероятность появления второго белого шара при условии, что была выбрана первая урна, и из нее вынут белый шар:

.

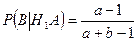Аналогично:

.

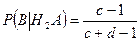В итоге:

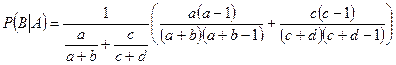. l