Формулы Муавра – Лапласа

Если в схеме Бернулли 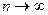, , 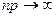, 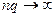(4.3.1)

то следует применять формулы Муавра – Лапласа: локальную или интегральную.

Локальная теорема Муавра‑Лапласа (без доказательства). Если в схеме Бернулли 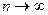, то для всех 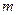справедлива локальная формула Муавра‑Лапласа:

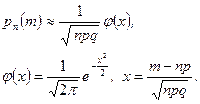(4.3.2)

Значения функции 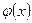, которую называют плотностью нормального распределения с параметрами 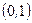, можно найти одним из следующих способов:

§ можно воспользоваться Приложением 2;

§ используя функцию НОРМРАСП(x;среднее;стандартное_откл;интегральная) из EXCEL; в которой «среднее» необходимо положить равным 0, аргумент «стандартное_откл» необходимо положить равным 1, аргумент «интегральная» должен равняться 0.

§ используя функцию dnorm(x, mu, sigma) из MATHCAD, в которой 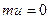и .

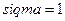Очевидно, что функция 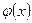является четной. Поэтому при определении 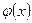для отрицательных 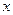нужно воспользоваться равенством .

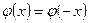Интегральная теорема Муавра‑Лапласа (без доказательства). Если в схеме Бернулли число испытаний 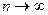, то для вероятности 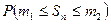того, что число успехов 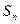заключено в пределах от 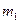до 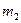, справедлива интегральная теорема Муавра‑Лапласа:

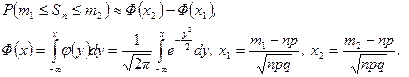(4.3.3)

Функция 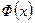, определенная формулой (4.3.3), называется функцией распределения нормального распределения с параметрами 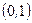. Значения функции 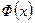можно найти одним из следующих способов:

§ можно воспользоваться Приложением 3;

§ используя функцию НОРМРАСП(x;среднее;стандартное_откл;интегральная) из EXCEL; в которой «среднее» необходимо положить равным 0, аргумент «стандартное_откл» необходимо положить равным 1, аргумент «интегральная» должен равняться 1.

§ используя функцию pnorm(x, mu, sigma)из MATHCAD, в которо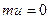й и .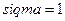

Функцию 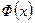при отрицательных значениях переменной можно определить по формуле .

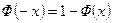Замечание.Нарядус функцией 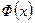используют функцию

. (4.3.4)

Для нее справедливо равенство ; она связана с функцией 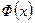равенством

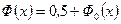. (4.3.5)

Пример 6.Симметричную монету бросают 400 раз. Определить вероятность появления герба:

а) от 185 до 210 раз;

б) ровно 200 раз;

в) не менее 200 раз.

m Решение.Для решения задачи применим локальную и интегральную теоремы Муавра‑Лапласа, для которых

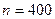, т.к. монету подбрасывали 400 раз, 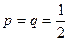, т.к. монета симметрична.

а) Используя интегральную теорему Муавра‑Лапласа, получим

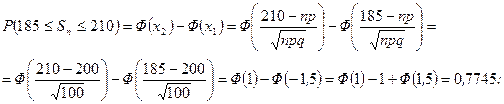
б) Используя локальную теорему Муавра‑Лапласа, получим

;

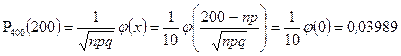в) Используя интегральную теорему Муавра‑Лапласа, получим

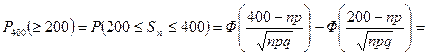
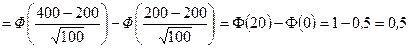. l

Пример 7. Команда состоит из 10 отличных и 15 хороших стрелков. Каждый стрелок производит по своей мишени 5 независимых выстрелов. Отличный стрелок при каждом выстреле попадает в цель с вероятностью 0,9, хороший — с вероятностью 0,8. Определить вероятность того, что общее число попаданий будет не менее 110.

m Решение. Найдем вероятность попадания при одном выстреле для произвольного стрелка. Для этого воспользуемся формулой полной вероятности. Пусть искомое событие 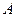— мишень поражена одним стрелком. Рассмотрим следующие гипотезы:

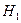— стреляет отличный стрелок;

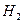— стреляет хороший стрелок.

Очевидно, что:

, , , .

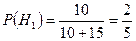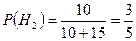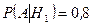Отсюда получаем:

, .

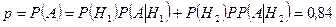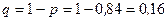Заметим, что общее число выстрелов

.

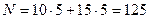Теперь найдем вероятность 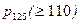того, что при 125 выстрелах число попаданий будет не менее 110. Для этого применим интегральную теорему Муавра‑Лапласа:

, ,

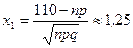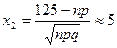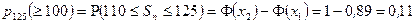. l

Пример 8. Вероятность попадания в мишень при одном выстреле 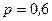. Найти наименьшее число выстрелов, которое надо произвести по мишени, чтобы с вероятностью 0,95 число попаданий было не менее 70.

m Решение. По условию задачи 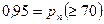. Для вычисления 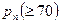применим интегральную теорему Муавра – Лапласа:

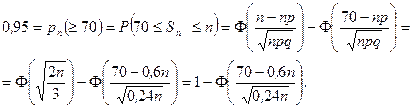
Заметим, что мы использовали то, что при больших значениях .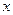

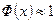Далее получаем

.

Используя Приложение 3 находим, что

.

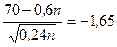Решая последнее уравнение для натуральных значений 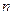, получаем, что n=132 . l