Дифференциальные операторы набла и Лапласа

Оператор набла (оператор Гамильтона) Ñ – это символический вектор, сочетающий в себе векторные и дифференцирующие свойства. Поэтому при действии с оператором Ñ необходимо применять правила векторной алгебры.

В декартовой системе координат оператор Ñ записывается:

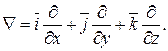
Существует запись его в цилиндрической и сферической системах координат.

При оперировании со сложными функциями используют правила дифференцирования сложных функций:

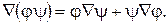(14.5)

Использование оператора Ñ позволяет упростить запись некоторых векторных операций. Так умножение оператора Ñ на скалярную функцию означает градиент этой функции

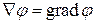. (14.6)

Скалярное умножение Ñ и вектора приводит к дивергенции вектора

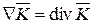. (14.7)

Векторное произведение Ñ на вектор дает ротор вектора

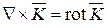. (14.8)

Оператор Лапласа 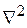(лапласиан) – это скалярный дифференциальный оператор, определяемый как дивергенция градиента скалярной функции (уравнение Лапласа ).

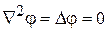В декартовой системе координат оператор 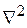запишется:

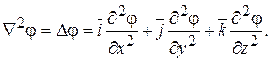(14.9)

Если применить оператор 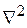к вектору 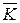, то

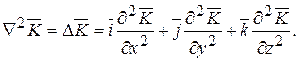(14.10)

где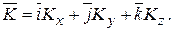

Векторное уравнение 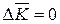можно представить тремя скалярными уравнениями:

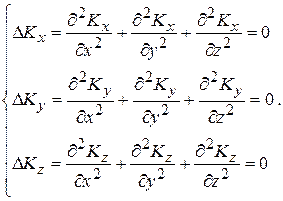(14.11)