Дифференциальные исчисления
1. Задача о касательной. Пусть на плоскости Оху дана непрерывная кривая y=f(x) и необходимо найти уравнение касательной к этой кривой в точке М0(х0, у0) (рис. 3.13).
|
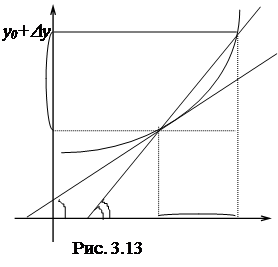 М1
М1
y=f(x)
Dy Dy=f(x0+Dx)–f(x0)
М0
y0  N
N
y0=f(x0)
y=f(x0+Dx)
a j Dx
О x0 x0+Dx x
секущей М0М1 при приближении точки М1 к точке М0, т. е. при Dх®0.
Уравнение прямой, проходящей через точку М0, имеет вид
y – f (x0) = k (x–x0).
Угловой коэффициент (или тангенс угла j наклона) секущей 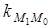 может быть найден из DM0M1N:
может быть найден из DM0M1N: 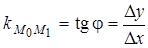 (см. рис. 3.13). Тогда угловой коэффициент касательной
(см. рис. 3.13). Тогда угловой коэффициент касательной
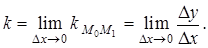 (3.3.1)
(3.3.1)
Оставим на время задачу о касательной и рассмотрим другую задачу.
2. Задача о скорости движения. Пусть вдоль некоторой прямой движется точка по закону s=s(t), где s – пройденный путь, t – время, и необходимо найти скорость точки в момент t0.
К моменту времени t0 пройденный путь равен s0=s(t0), а к моменту (t0+Dt) – путь s0+Ds=s (t0+Dt) (рис. 3.14).
|
s(t0) Ds s(t0+Dt)

t0 Dt t0+Dt t
Рис. 3.14
понимать предел средней скорости за промежуток от t0 до t0+Dt, когда Dt®0, т.е.
 (3.3.2)
(3.3.2)
Рассматривая две различные по характеру задачи, мы пришли к пределу (3.3.1) и (3.3.2) одного вида. Этот предел играет чрезвычайно важную роль в математическом анализе, являясь основным понятием дифференциального исчисления.
Пусть функция y=f(x) определена на промежутке Х. Возьмем точку хÎХ. Дадим значению х приращение Dх¹0, тогда функция получит приращение Dy=f(x+Dx)–f(x).
Определение. Производной функции y=f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
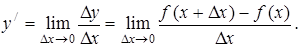 (3.3.3)
(3.3.3)
Производная функции имеет несколько обозначений: y/, f / (x), 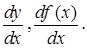 Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например, у /x.
Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например, у /x.
Нахождение производной функции называется дифференцированием этой функции.
Если функция в точке х имеет конечную производную, то функция называетсядифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.
Теперь вернемся к рассмотренным выше задачам.
Из задачи о касательной вытекает геометрический смысл производной: производная f / (x0) есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой y=f(x) в точке х0, т. е. k=f¢(x0).
Тогда уравнение касательной к кривой y=f(x) в точке х0 примет вид
y – f (x0) = f / (x0) (x–x0). (3.3.4)
Из задачи о скорости движения следует механический смыслпроизводной: производная пути по времени s /(t0) есть скорость точки в момент t0: v(t0) = s /(t0).
Зависимость между непрерывностью функции и дифференцируемостью. Теорема. Если функция y=f(x) дифференцируема в точке х0, то она в этой точке непрерывна.
Обратная теорема, вообще говоря, не верна, т. е. если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке.
Таким образом, непрерывность функции – необходимое, но недостаточное условие дифференцируемости функции.
В математике известны непрерывные функции, но не дифференцируемые ни в одной точке.
Замечание. Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором промежутке Х, то функция называется гладкой на этом промежутке. Если же производная функция допускает конечное число точек разрыва (причем первого рода), то такая функция на данном промежутке называется кусочно гладкой.
Дата добавления: 2015-06-17; просмотров: 936;

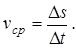 Чем меньше Dt, тем лучше средняя скорость характеризует движение точки в момент t0. Поэтому под скоростью точки в момент t0 естественно
Чем меньше Dt, тем лучше средняя скорость характеризует движение точки в момент t0. Поэтому под скоростью точки в момент t0 естественно