Понятие о градиенте, дивергенции и роторе

Градиент скалярной функции – это вектор, указывающий направление наиболее быстрого возрастания скалярной функции и по абсолютному значению равный наибольшей скорости возрастания этой функции.

(14.12)

Градиент направлен по нормали к поверхности равного уровня скалярной функции в данной точке. Градиент скалярного потенциала j постоянного во времени поля равен:

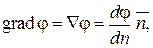(14.13)

где 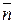– нормаль к эквипотенциальной поверхности в данной точке поля.

Градиент скалярного потенциала j в каждой точке совпадает с касательной к силовой линии напряженности электрического поля 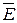в данной точке и имеет направление, противоположное вектору 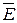(рис. 14.3).

Дивергенция (расхождение вектора) – это алгебраическая скалярная величина, характеризующая источники поля в рассматриваемой точке поля или указывающая на отсутствие источников

.

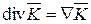Численно дивергенцию в данной точке определяют как предел, к которому стремится отношение потока вектора через замкнутую поверхность к объему, ограниченному этой поверхностью, при стремлении этого объема к нулю

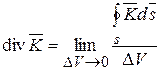. (14.14)

Если div 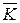> 0, то имеются источники поля и линии вектора 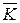расходятся из данной точки. Точка наблюдения служит началом (истоком) линий вектора .

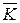Если div 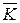< 0, то в точке наблюдения линии вектора 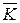сходятся, т.е. она служит стоком линий вектора .

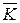Если div 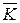= 0, то в рассматриваемой точке отсутствует источник линий вектора .

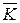Картина электрического поля при наличии и отсутствии зарядов показана на рис. 14.4. Например, если имеется объемный положительный заряд +r, то он является истоком вектора электрического смещения .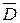

Дивергенция вектора магнитной индукции 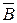всегда равна нулю, так как линии вектора 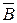замкнуты (не имеют начала и конца).

В декартовой системе координат

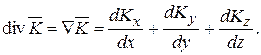(14.15)

Ротор (вихрь) вектора поля rot 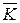– это вектор, характеризующий интенсивность вихревых полей в каждой точке. Ротор проявляет себя как вихрь, поэтому он имеет ось. Направление оси определяет направление вектора, изображающего ротор.

Численно составляющую ротора в направлении нормали 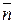к плоской площадке Ds определяют как предел, к которому стремится отношение циркуляции вектора к площадке Ds, ограниченной контуром интегрирования, при стремлении ее к нулю (рис. 14.5)

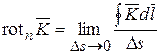. (14.16)

Если вихревое поле в некоторой области не имеет внутри источников векторных линий, то rot 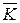¹ 0 (div 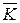= 0).

Запишем ротор вектора в декартовой системе координат

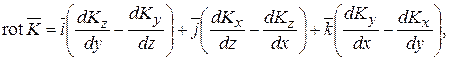(14.17)

где: 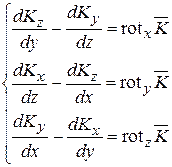. (14.18)

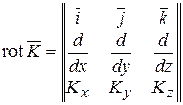(14.19)

14.1.4. Запись основных векторных операций с помощью оператора Ñ

Пространственные производные grad, div и rot можно записать с помощью оператора Ñ. При этом умножение оператора Ñ на скалярную функцию равносильно взятию градиента этой функции Ñj = grad j. Скалярное умножение оператора Ñ и вектора дает дивергенцию этого вектора 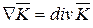, а векторное их умножение образует ротор вектора 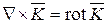. Применение оператора Ñ облегчает выполнение сложных векторных операций. В табл.14.1 приведены примеры символической записи наиболее часто встречающихся векторных операций.