Линейный, поверхностный и объемный интегралы

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ

ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Основные операторы и векторные операции

Электромагнитное поле – это вид материи, определяемый во всех точках двумя векторными величинами, которые характеризуют две его стороны, называемые электрическим полем и магнитным полем, и оказывающий силовое воздействие на заряженные частицы, зависящее от их скорости и заряда (ГОСТ 19880-74).

Основным математическим аппаратом при расчете электромагнитного поля является векторный анализ, включающий в себя понятия: скаляр, вектор и тензор. В общем случае скаляры и векторы являются функциями координат точки и времени. При анализе электромагнитного поля применяют линейный, поверхностный и объемный интегралы, а также дифференциальные операторы.

Оператор – это символ, характеризующий действие над вектором или скаляром, расположенным после символа.

Дифференциальные операторы позволяют сократить запись различных операций над скалярными и векторными величинами.

Линейный, поверхностный и объемный интегралы

Пусть имеется кривая l, ограничивающая поверхность S, которая находится в электромагнитном поле (рис. 14.1).

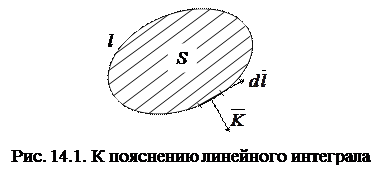Линейный по кривой l интеграл является скалярной величиной

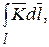(14.1)

где 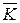– вектор электромагнитного поля.

Вектор 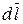имеет направление, касательное к элементу кривой интегрирования l.

Циркуляцией вектора 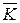по замкнутой кривой l называется интеграл вида: 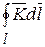. (14.2)

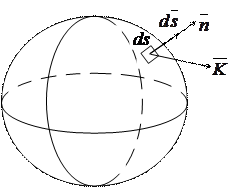
Поверхностный интеграл по поверхности S (рис. 14.2) имеет вид:

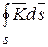. (14.3)

	Рис. 14.2. К пояснению поверхностного интеграла

Его часто называют потоком вектора 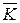через поверхность S.

Вектор 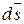имеет направление, совпадающее с направлением внешней нормали 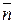к элементу замкнутой поверхности. Он численно равен элементу поверхности ds.

Объемный интеграл по объему V:

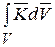. (14.4)

Элемент объема 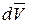– это физически бесконечно малый объем, который может иметь форму куба, сферы и т.д.