Поверхностные интегралы первого и второго рода, их основные свойства и вычисление.

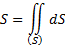
 – задание поверхности.
– задание поверхности.
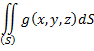
Спроектируем S на плоскость xy, получим область D. Разобьём область D сеткой линий на части, называемые Di. Из каждой точки каждой линии проведём параллельные z линии, тогда и S разделится на Si. Составим интегральную сумму: 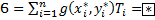 . Устремим максимум диаметра Di к нулю:
. Устремим максимум диаметра Di к нулю: 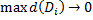 , получим:
, получим:
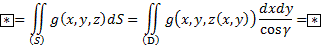
Это поверхностный интеграл первого рода

Так считается поверхностный интеграл первого рода.
Определение вкратце. Если существует конечный предел интегральной суммы, не зависящий от способа разбиения S на элементарные участки Si и от выбора точек, то он называется поверхностным интегралом первого рода.
При переходе от переменных x и y к u и v:
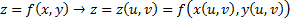
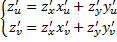
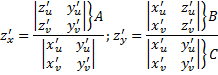
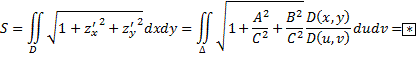

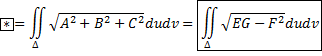
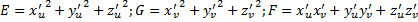
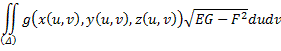
 Поверхностный интеграл обладает всеми свойствами обычного интеграла. См. в вопросах выше.
Поверхностный интеграл обладает всеми свойствами обычного интеграла. См. в вопросах выше.
Определение поверхностного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.
Пусть задана поверхность S, ограниченная линией L (рис. 3.10). Возьмём на поверхности S какой-нибудь контур L, не имеющий общих точек с границей L. В точке М контура L можно восстановить две нормали 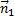 и
и  к поверхности S. Выберем какое-либо одно из этих направлений. Обводим точку M по контуру L с выбранным направлением нормали.
к поверхности S. Выберем какое-либо одно из этих направлений. Обводим точку M по контуру L с выбранным направлением нормали.
Если в исходное положение точка M вернётся с тем же направлением нормали (а не с противоположным), то поверхность S называют двусторонней. Мы будем рассматривать только двусторонние поверхности. Двусторонней поверхностью является всякая гладкая поверхность с уравнением 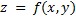 .
.
Пусть S – двусторонняя незамкнутая поверхность, ограниченная линией L, не имеющей точек самопересечения. Выберем определённую сторону поверхности. Будем называть положительным направлением обхода контура L такое направление, при движении по которому по выбранной стороне поверхности сама поверхность остаётся слева. Двусторонняя поверхность с установленным на ней таким образом положительным направлением обхода контуров называется ориентированной поверхностью.
Перейдём к построению поверхностного интеграла второго рода. Возьмём в пространстве двустороннюю поверхность S, состоящую из конечного числа кусков, каждый из которых задан уравнением вида 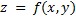 или является цилиндрической поверхностью с образующими, параллельными оси Oz.
или является цилиндрической поверхностью с образующими, параллельными оси Oz.
Пусть R(x,y,z) – функция, опредёленная и непрерывная на поверхности S. Сетью линий разбиваем S произвольным образом на n "элементарных" участков ΔS1, ΔS2, ..., ΔSi, ..., ΔSn, не имеющих общих внутренних точек. На каждом участке ΔSi произвольным образом выберем точку Mi(xi,yi,zi) (i=1,...,n). Пусть (ΔSi)xy – площадь проекции участка ΔSi на координатную плоскость Оху, взятая со знаком "+", если нормаль к поверхности S в точке Mi(xi,yi,zi) (i=1,...,n) образует с осью Oz острый угол, и со знаком "–", если этот угол тупой. Составим интегральную сумму для функции R(x,y,z) по поверхности S по переменным x,y:  . Пусть λ – наибольший из диаметров ΔSi (i = 1, ..., n).
. Пусть λ – наибольший из диаметров ΔSi (i = 1, ..., n).
Если существует конечный предел 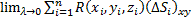 , не зависящий от способа разбиения поверхности S на "элементарные" участки ΔSi и от выбора точек
, не зависящий от способа разбиения поверхности S на "элементарные" участки ΔSi и от выбора точек 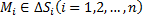 , то он называется поверхностным интегралом по выбранной стороне поверхности S от функции R(x,y,z) по координатам х, у (или поверхностным интегралом второго рода) и обозначается
, то он называется поверхностным интегралом по выбранной стороне поверхности S от функции R(x,y,z) по координатам х, у (или поверхностным интегралом второго рода) и обозначается 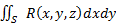 .
.
Аналогично можно построить поверхностные интегралы по координатам x, z или у, z по соответствующей стороне поверхности, т. е. 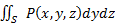 и
и 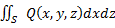 .
.
Если существуют все эти интегралы, то можно ввести "общий" интеграл по выбранной стороне поверхности: 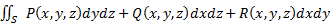 .
.
Поверхностный интеграл второго рода обладает обычными свойствами интеграла. Заметим лишь, что любой поверхностный интеграл второго рода изменяет знак при перемене стороны поверхности.
Связь между поверхностными интегралами первого и второго рода.
Пусть поверхность S задана уравнением: z = f(x,y), причем f(x,y), f'x(x,y), f'y(x,y) — непрерывные функции в замкнутой области τ (проекции поверхности S на координатную плоскость Оху), а функция R(x,y,z) непрерывна на поверхности S. Нормаль к поверхности S, имеющая направляющие косинусы cos α, cos β, cos γ, выбрана к верхней стороне поверхности S. Тогда 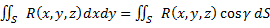 .
.
Для общего случая имеем:

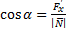 =
= 
Теорема Гаусса-Остроградского, ее запись в координатной и векторной (инвариантной) формах.
 В координатной форме. Рассмотрим тело (V) в пространстве с ограничивающей поверхностью (S).
В координатной форме. Рассмотрим тело (V) в пространстве с ограничивающей поверхностью (S).
Рассмотрим некую функцию R(x,y,z), заданную в области (V) и на границе, непрерывную в этой области и на границе вместе со своими частными производными первого порядка. Рассмотрим интеграл 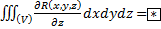 . Спроецируем тело на область D. Возьмём точку (x,y).
. Спроецируем тело на область D. Возьмём точку (x,y).
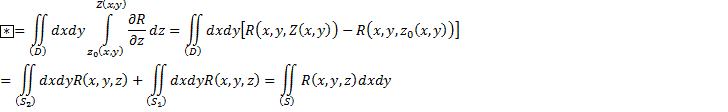
 Сделаем то же самое, но с проекцией на оси y и z.
Сделаем то же самое, но с проекцией на оси y и z.

Теперь спроектируем на оси x и z.

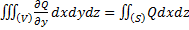
Складывая эти формулы, получаем формулу Остроградского-Гаусса: 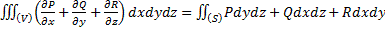 . Формула сводит интеграл от объёма к интегралу по границе.
. Формула сводит интеграл от объёма к интегралу по границе.
Если 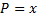 и
и 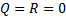 или
или 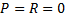 и
и 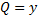 или
или 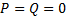 и
и 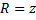 , тогда
, тогда 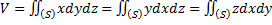 . А если
. А если 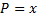 ,
, 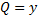 и
и 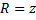 , то:
, то: 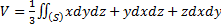 .
.
В общем виде теорема звучит так. Пусть в замкнутой ограниченной области (V) заданы функции P(x,y,z), Q(x,y,z) и R(x,y,z), непрерывные на (V) вместе со своими частными производными первого порядка. Тогда имеет место следующее тождество: 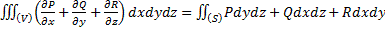 .
.
 Запись формулы в векторном виде. Пусть
Запись формулы в векторном виде. Пусть 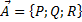 . В обычном виде формула выглядит так:
. В обычном виде формула выглядит так: 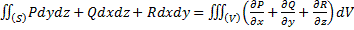
Левую часть можно записать так: 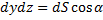 ,
, 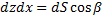 ,
, 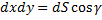 . Следовательно:
. Следовательно: 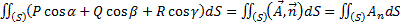 , так как
, так как 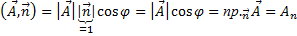 . Мы получили поток вектора через замкнутую поверхность. Правую часть можно записать как дивергенцию (расходимость):
. Мы получили поток вектора через замкнутую поверхность. Правую часть можно записать как дивергенцию (расходимость): 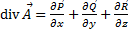 . В итоге формула Гаусса-Остроградского в векторном виде:
. В итоге формула Гаусса-Остроградского в векторном виде: 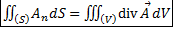 . Читается так: поток вектора через замкнутую поверхность равен интегралу по объёму от его дивергенции.
. Читается так: поток вектора через замкнутую поверхность равен интегралу по объёму от его дивергенции.
Дивергенцией векторного поля A в точке MÎV называется производная функции 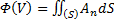 по объему в этой точке:
по объему в этой точке:  .
.
Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.
 .
. 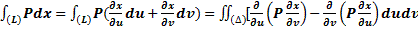 {ф. Грина}=
{ф. Грина}=
= 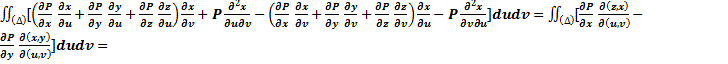
 . Аналогично
. Аналогично 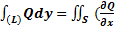 c
c  ,
, 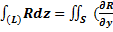 c
c 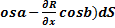 .
.
Теорема: Пусть в некоторой окрестности поверхности S функции Р(х, у, z), Q(x, у, z) и R(x, у, z) непрерывны и имеют непрерывные частные, производные первого порядка. Тогда имеет место следующее соотношение:
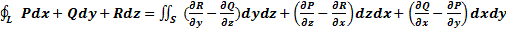 . (Формула Стокса).
. (Формула Стокса).
 .
.
Инвариантная запись формулы Стокса: Используя выражение для 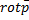 в ортогональном базисе
в ортогональном базисе 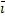 ,
, 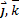 :
:
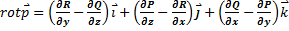 . Укажем на поверхности S определенную сторону, т.е. укажем непрерывное поле единичных нормалей
. Укажем на поверхности S определенную сторону, т.е. укажем непрерывное поле единичных нормалей  . Используя стандартное обозначение cosx, cosy, cos
. Используя стандартное обозначение cosx, cosy, cos 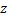 для координат единичного вектора нормали
для координат единичного вектора нормали  к поверхности S получим:
к поверхности S получим: 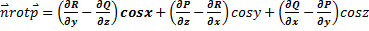 . Из соотношения видно, левая часть формулы Стокса может быть записана в виде
. Из соотношения видно, левая часть формулы Стокса может быть записана в виде 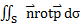 . Скалярное произведение:
. Скалярное произведение: 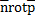 и элемент площади
и элемент площади 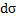 поверхности S не зависят от выбора декартовой прямоугольной системы координат в пространстве, и при переходе к новому ортогональному базису
поверхности S не зависят от выбора декартовой прямоугольной системы координат в пространстве, и при переходе к новому ортогональному базису 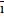 ',
', 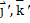 левая часть формулы не изменит своего значения и формы – инвариантна.
левая часть формулы не изменит своего значения и формы – инвариантна.
Рассмотрим 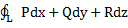 . Пусть
. Пусть 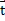 – единичный вектор касательной в точках границы L поверхности S, cosa, cosb, cos
– единичный вектор касательной в точках границы L поверхности S, cosa, cosb, cos 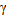 – координаты этого вектора.
– координаты этого вектора. 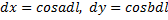 ,
, 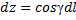 . Т.о
. Т.о 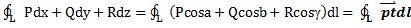 – циркуляция векторного поля p по кривой L.
– циркуляция векторного поля p по кривой L.  - инвариант. Получаем
- инвариант. Получаем 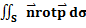 =
= 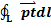 .
.
Дата добавления: 2015-05-16; просмотров: 2661;
