Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
 Формула Грина: Если C – замкнутая граница области D и функции P(x,y) и Q(x,y) вместе со своими частными производными первого порядка
Формула Грина: Если C – замкнутая граница области D и функции P(x,y) и Q(x,y) вместе со своими частными производными первого порядка  непрерывны в замкнутой области D (включая границу C), то справедлива формула Грина:
непрерывны в замкнутой области D (включая границу C), то справедлива формула Грина:  , причем обход вокруг контура C выбирается так, что область D остается слева.
, причем обход вокруг контура C выбирается так, что область D остается слева.
Из лекций: Пусть заданы функции P(x,y) и Q(x,y), которые непрерывны в области D вместе с частными производными первого порядка. Интеграл по границе (L), целиком лежащий в области D и содержащий все точки в области D:  . Положительное направление контура такое, когда ограниченная часть контура находится слева.
. Положительное направление контура такое, когда ограниченная часть контура находится слева.
 Условие независимости криволинейного интеграла 2-го рода от пути интегрирования. Необходимым и достаточным условием того, что криволинейный интеграл первого рода, соединяющий точки M1 и M2, не зависит от пути интегрирования, а зависит только от начальной и конечной точек, является равенство:
Условие независимости криволинейного интеграла 2-го рода от пути интегрирования. Необходимым и достаточным условием того, что криволинейный интеграл первого рода, соединяющий точки M1 и M2, не зависит от пути интегрирования, а зависит только от начальной и конечной точек, является равенство: 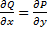 .
.
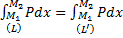 .
.
 .
.
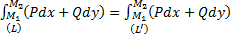 .
.
Дата добавления: 2015-05-16; просмотров: 2560;
