Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.

Скалярное поле. Градиент скалярного поля и его свойства. Вычисление градиента в декартовых координатах.

Пусть D – область на плоскости или в пространстве. Говорят, что в D задано скалярное поле, если каждой точке области D ставится в соответствие некая функция U(M).

Определение по-другому. Скалярное поле определяется скалярной функцией точки 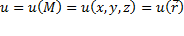, где M(x,y,z) – точка пространства, 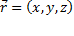– её радиус-вектор.

Определение градиента. Градиентом скалярной функции u(M), определенной и дифф в некоторой области D, называется вектор 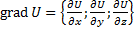. . 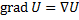Знак 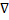- это вектор Набла.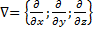

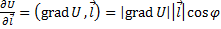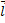( – единичный вектор с координатами: ).

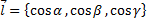Из последнего выражения видно, что 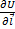максимально, когда 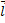совпадает с направлением градиента. Следовательно, градиент показывает направление наибольшего изменения скорости функции.

Градиент скалярного поля – вектор.

Свойства градиента:

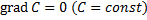
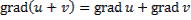
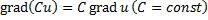
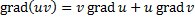
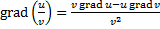
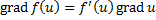
Векторное поле. Если каждой точке М некоторой области V пространства соответствует значение некоторой векторной величины 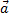(M), то говорят, что в области V задано векторное поле 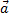(M). Примеры векторных полей – поле тяготения, поля электрической и магнитной напряжённостей, поле скоростей частиц движущейся жидкости.

Если в некоторой декартовой системе координат вектор 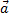(M) имеет координаты Р(M), Q(M), R(M), то 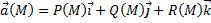. Таким образом, задание векторного поля 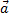(M) эквивалентно заданию трёх скалярных полей Р(M), Q(M), R(M). Будем называть векторное поле гладким, если его координатные функции - гладкие скалярные поля.

Градиентом дифференцируемого скалярного поля u(M)=u(x,y,z) называется вектор 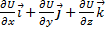. Т.е. сумма частных производных умноженных на соответствующие единичные вектора.

В общем случае градиент вводится как векторная характеристика скалярного поля — то есть области, каждой точке которой соответствует значение определенного скаляра. Градиент характеризует, насколько быстро меняется скалярная величина в том или ином месте этого поля.

Потенциальные векторные поля. Векторное поле A = {Ax, Ay, Az} называется потенциальным, если вектор А является градиентом некоторой скалярной функции u = u(x, y, z): A = grad u = 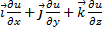(16.7).

При этом функция u называется потенциалом данного векторного поля.

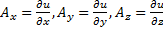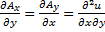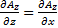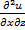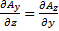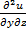Выясним, при каких условиях векторное поле является потенциальным. Так как из (16.7) следует, что , То , = , = . так как смешанная производная второго порядка не зависит от порядка дифференцирования. Из этих равенств легко получаем, что rot A = 0 -условие потенциальности векторного поля.

Ротором векторного поля 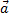(M) в точке 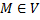называется векторная величина (векторное поле): 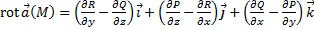. Если выразить 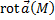через оператор Гамильтона набла: 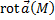равен векторному произведению 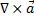. Действительно, .

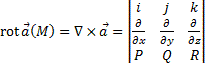Пусть в некоторой области D задано непрерывное векторное поле 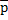(M)= 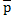(x,y,z). Потоком векторного поля 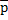через ориентированную кусочно-гладкую поверхность S, расположенную в области D, называется интеграл 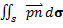, где 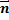– единичный вектор нормали к поверхности S, указывающий на ее ориентацию, а 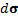– элемент площади поверхности S.

Векторное поле 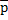называется соленоидальным в области D, если поток этого поля через любую кусочно-гладкую несамопересекающуюся поверхность, расположенную в D и представляющую собой границу некоторой ограниченной подобласти области D, равен нулю.

Если дивергенция равна нулю, то есть 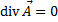, то поле вектора 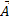называется соленоидальным.

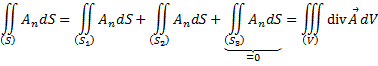
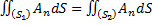, поэтому поток везде, на каждом сечении трубки, одинаков.

Для того чтобы непрерывно дифференцируемое векторное поле 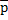было соленоидальным в объемно-односвязной области D, необходимо и достаточно, чтобы во всех точках D выполнялось равенство 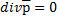. Где дивергенцией (“расходимость”) векторного поля 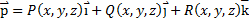называется скалярная функция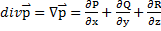

Циркуляцией векторного поля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру L: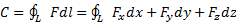

Где 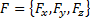— векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур L, 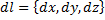— бесконечно малое приращение радиус-вектора 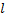вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру.

Циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую поверхность в отдельности, то есть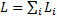

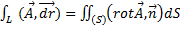– формула Стокса в векторном виде.

Вихревым вектором (вихрем) или ротором векторного поля 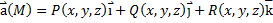называется вектор, имеющий координаты: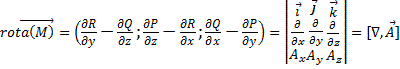

Ротор в декартовых координатах: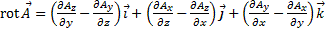

Если 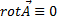, то векторное поле 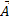называется безвихревым или потенциальном.