Интегрирование ОДУ первого порядка с разделяющимися переменными и однородных.

Уравнением с разделенными переменными называется дифференциальное уравнение вида: 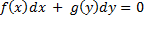с непрерывными функциями f(х) и g(y). Равенство 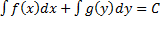, где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.

Принцип решения таких уравнений: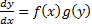

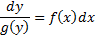
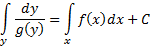
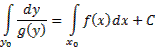
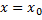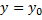Если дано условие Коши, то есть и , то 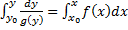. Если 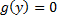и уравнение имеет корень 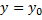, то это решение добавляется к основному семейству.

Определение однородной функции. Функция f(x,y) называется однородной функцией своих переменных x и y, если, каково бы ни было число 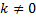, выполняется следующее: 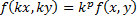, где p – степень (показатель) однородности. Например, 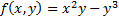– однородная функция, степень однородности 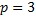, так как 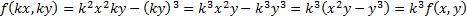. Степень p может быть равной нулю, если .

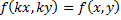Уравнение 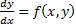называется однородным, если функция, стоящая в правой части, является однородной функцией своих переменных. Пусть f(x,y) будет однородной функцией степени 0, то есть 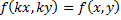. Пусть 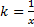, тогда 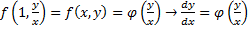. Уравнения такого типа решаются заменой (переходом к новой функции): .

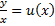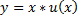
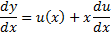
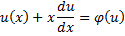
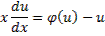
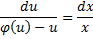
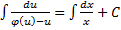– общее решение.

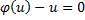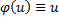Если , а , то: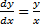

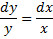
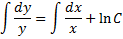
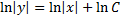
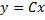
Если 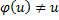, то уравнение 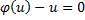имеет корень u0, тогда: 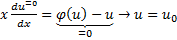– решение: 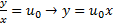– прямая наряду с семейством.

Общий вид однородного уравнения, если его записать в виде дифференциалов: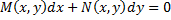

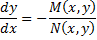
То есть M(x,y) и N(x,y) должны быть однородными функциями одной и той же степени однородности.