Виды фазовых портретов для линейных систем второго порядка

Корни характеристического уравнения	Переходный процесс	Фазовая траектория

1. a₁=0, a₂>0
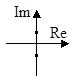
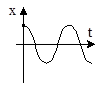
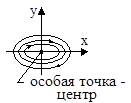
2. a₁²>4a₂, a₁>0, a₂>0

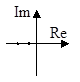
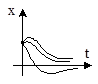
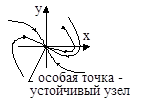
Продолжение табл.


3. a₂<0
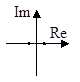
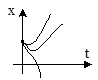
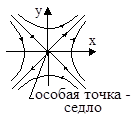
4. a₁²<4a₂, a₁<0, a₂>0
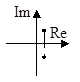
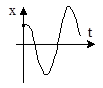
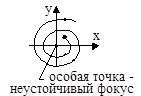
5. a₁²<4a₂, a₁>0, a₂>0
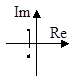
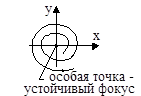
6. a₁²>4a₂, a₁<0, a₂>0

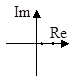
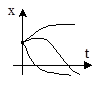
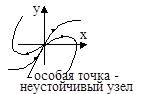
Вид и расположение фазовых траекторий, а также направление движения по ним изображающей точки дают возможность судить о характере движения системы и его устойчивости при различных начальных отклонениях. Особые точки и их характер определяют состояние равновесия исходной системы.

Реальные автоматические системы можно считать линейными в предположении малости отклонений переменных от их установившихся значений. За пределами указанной области картина фазовых траекторий может стать качественно иной. В частности, если по линейной теории система неустойчивая и процесс расходится, то может оказаться, что из-за фактической нелинейности характеристик он не будет расходящимся неограниченно. Картина фазовых траекторий для такой системы изображена на рис. 2.15,а. Здесь вблизи начала координат получаются спирали, как в неустойчивой линейной системе, но далее они приближаются асимптотически к замкнутому контуру ограниченных размеров. К нему же приближаются и все спирали, находящиеся вне контура. Такого рода замкнутый контур представляет собой особый вид линий на фазовой плоскости и называется устойчивым предельным циклом. Устойчивый предельный цикл соответствует автоколебаниям системы. Размеры предельного цикла представляют амплитуды колебаний самой величины x и скорости ее изменения y. Для определения периода автоколебаний необходимо решить уравнение системы во времени.

Рис. 2.15. Фазовые траектории нелинейных систем:

а - устойчивый предельный цикл; б - неустойчивый предельный цикл;

в - фазовый портрет системы с сепаратрисами

Замкнутые фазовые траектории на фазовой плоскости называются предельными циклами, которые могут быть как устойчивыми (рис. 2.15,а), так и неустойчивыми (рис. 2.15,б). К этим предельным циклам стремятся изображающие точки при различных начальных отклонениях по различным фазовым траекториям.

В различных частях фазовой плоскости фазовые траектории нелинейной системы могут быть различными (рис. 2.15,в). Линии, разделяющие фазовую плоскость на участки с различными фазовыми траекториями, называются сепаратрисами. Поведение системы в каждой области фазовой плоскости описывается своим дифференциальным уравнением.

Кроме того, для фазового портрета нелинейных систем с разрывными характеристиками характерно наличие линий переключения, которые также разделяют фазовую плоскость на ряд областей с различными фазовыми траекториями. При этом начальные значения переменных на каждом участке определяются через их конечные значения на предыдущем участке. Линии переключения характеризуются узловыми точками разрывных характеристик нелинейных элементов.

Замечание: координатами (x, y) фазовой плоскости могут служить не обязательно отклонение (ошибка) управляемой величины системы и ее скорость. Для этой цели могут быть взяты любые две переменные, однозначно характеризующие состояние системы второго порядка в произвольный момент времени.

Пример. Изобразим на фазовой плоскости переходный процесс и автоколебания в автоматической системе (рис. 2.1), линейная часть которой задана передаточной функцией

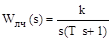где k - коэффициент передачи;

T - постоянная времени,

а нелинейный элемент - статической характеристикой y_н = F(x).

Р е ш е н и е. В качестве координат фазовой плоскости выбираем отклонение управляемой величины x и скорость ее изменения y = dx/dt. Запишем для ошибки x дифференциальное уравнение системы, описывающее ее свободное движение

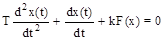, (2.42)

которое заменяем эквивалентными уравнениями первого порядка

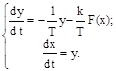(2.43)

Разделив первое из уравнений (2.43) на второе, получаем дифференциальное уравнение фазовых траекторий

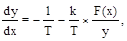(2.44)

решение которого определяется характеристикой нелинейного элемента.

Рассмотрим фазовые портреты системы для некоторых типов нелинейных элементов.

1. Идеальное двухпозиционное реле (рис. 2.4,а) со статической характеристикой F(x) = csign(x).

Дифференциальное уравнение (2.44) фазовых траекторий в этом случае примет вид

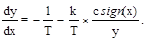(2.45)

Переключение идеального реле происходит при x = 0. Следовательно, линия переключения на фазовой плоскости (рис. 2.16,а) совпадает с осью ординат.

Справа от линии переключения при x > 0 дифференциальное уравнение фазовых траекторий будет

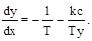(2.46)

Его интегрирование дает уравнение фазовой траектории [2]

x = kcT ln½y + kc½ - Ty + c⁰, (2.47)

где c⁰- постоянная интегрирования, определяемая начальными условиями. Каждому конкретному c⁰соответствует определенная кривая на фазовой плоскости справа от линии переключения. Эти кривые имеют асимптоту y = -kc.

Слева от линии переключения при x < 0 дифференциальное уравнение (2.45) фазовых траекторий принимает вид

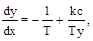(2.48)

что дает решение [2]

x = -kcT ln½y - kc½ - Ty + c⁰, (2.49)

согласно которому наносится семейство фазовых траекторий с асимптотой y = kc в левой фазовой полуплоскости.

На рис. 2.16,а изображены фазовые траектории системы для начальных условий (x₀, 0).

Рис. 2.16. Фазовые траектории релейных систем:

а - с идеальным реле; б - с реле с гистерезисом

2. Двухпозиционное реле с гистерезисом (рис. 2.4,в) со статической характеристикой

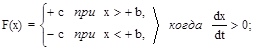
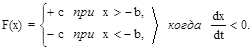
Переключение реле с гистерезисом происходит при x = +b, если y > 0 (линия AB на рис. 2.16,б); если же y < 0, то при x = -b (линия CD). Соответственно, линия переключения ABCD на фазовой плоскости (рис. 2.16,б) имеет разрыв.

Справа от линии переключения ABCD справедливо дифференциальное уравнение фазовых траекторий (2.46), а слева - (2.48). Следовательно, фазовые траектории рассматриваемой системы (рис. 2.16,б) строятся аналогично предыдущему случаю.

В данной системе будут наблюдаться устойчивые автоколебания, к которым сходится переходный процесс с обеих сторон, т.е. при любых начальных условиях. Амплитуда автоколебаний изображена на рис. 2.16,б отрезком a; отрезок y_M изображает амплитуду скорости. Период автоколебаний определяется решением уравнений во времени.

3. Трехпозиционное реле с зоной нечувствительности (рис. 2.4,б) со статической характеристикой

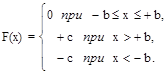
Переключение трехпозиционного реле с зоной нечувствительности происходит при x = -b (линия AB фазовой плоскости на рис. 2.17,а) и при x = +b (линия CD). Соответственно, линии переключения AB и CD разделяют фазовую плоскость на на три области (рис. 2.17,а).

Справа от линии переключения CD справедливо дифференциальное уравнение фазовых траекторий (2.46), а слева от линии переключения AB - (2.48). Следовательно, для рассматриваемой системы фазовые траектории в этих областях фазовой плоскости (рис. 2.17,а) строятся аналогично предыдущим случаям.

В средней области при -b £ x £ +b, соответствующей зоне нечувствительности реле, дифференциальное уравнение (2.44) фазовых траекторий принимает вид

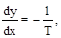(2.50)

откуда

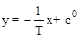, (2.51)

согласно которому семейство фазовых траекторий образуется отрезками прямых линий с отрицательным угловым коэффициентом -1/T.

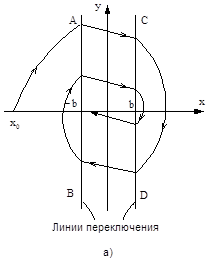
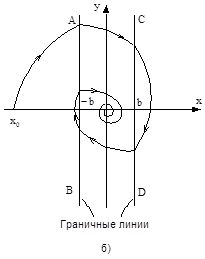
Рис. 2.17. Фазовые траектории нелинейных систем:

а - с трехпозиционным реле; б – с усилителем с насыщением

На рис. 2.17,а изображены фазовые траектории системы для начальных условий (x₀, 0). Система приходит в положение равновесия при значениях ошибки, определяемой зоной нечувствительности реле.

4. Усилитель с насыщением (рис. 2.3,а) со статической характеристикой

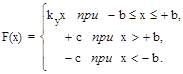
Для построения фазовых траекторий нелинейной системы с кусочно-линейной характеристикой нелинейного элемента фазовую плоскость разделяем на области линиями AB и CD (рис. 2.17,б).

Как следует из сравнения статических характеристик нелинейных элементов, фазовые траектории в правой и левой областях фазовой плоскости рассматриваемой системы строятся аналогично предыдущему случаю.

В средней области при -b £ x £ +b, соответствующей линейному участку характеристики, система становится линейной и дифференциальное уравнение (2.44) фазовых траекторий принимает вид

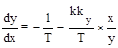. (2.52)

На рис. 2.17,б приведена фазовая траектория системы для начальных условий (x₀, 0) в случае ее устойчивости в линейной области.

Метод точечных преобразований (метод Пуанкаре-Андронова) позволяет установить существование автоколебаний в нелинейной системе второго порядка без построения фазовых траекторий [10]. Сущность метода заключается в том, что для исследования динамики системы необходимо выяснить, как в зависимости от начальных условий перемещаются точки пересечения фазовой траектории с некоторой полупрямой, например, отрезком 0X фазовой плоскости (рис. 2.18).

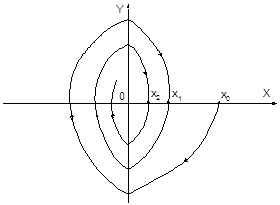
Рис. 2.18. Фазовая плоскость

Возьмем начальное положение изображающей точки (x₀, 0) где-нибудь на полуоси 0X. После обхода вокруг начала координат изображающая точка пересекает полуось 0X в точках x₁, x₂и т.д. Последовательность точек пересечения фазовой траектории с выбранной полупрямой представляет точечное преобразование полупрямой самой в себя. Задавая различные начальные положения x₀_i изображающей точки на полуоси 0X, согласно уравнениям системы определяют соответствующие им точки x_iна той же полуоси после обхода начала координат. Полученная таким образом зависимость

x_i = f(x₀_i) (2.53)

называется функцией соответствия и используется для исследования периодических режимов в нелинейных системах.

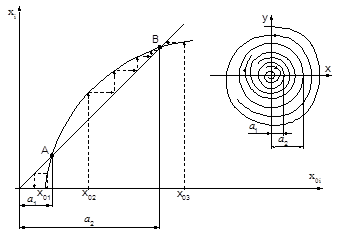
Рис. 2.19. Функция соответствия

Для исследования возможных автоколебаний в координатах функции соответствия (рис. 2.19) проводится прямая из начала координат под углом 45⁰к координатным осям, для которой x_i = x₀_i, что соответствует отображению каждой точки полуоси 0X самой в себя, т.е. после обхода вокруг начала координат точка возвращается в исходное положение. Пересечение кривой x_i = f(x₀_i) с прямой x_i = x₀_i (точки A и B) определяют существование предельного цикла. Если указанная кривая и прямая не пересекаются, то автоколебания невозможны, а если касаются, то имеет место один предельный цикл.

Чтобы определить, какому типу предельного цикла это соответствует, надо взять на оси абсцисс начальную точку x₀сначала слева, а затем справа от точки пересечения и проследить ход точечного преобразования, как показано стрелками на рис. 2.19.

Рис. 2.19 соответствует двум предельным циклам, из которых меньший (точка A) неустойчив, а больший (точка B) устойчив. Следовательно, при начальных условиях (x₀, y₀), расположенных внутри меньшего предельного цикла, система устойчива, а при всяких других начальных условиях она стремится к установившемуся автоколебательному процессу.

ложение. Пересечение кривой x_i = f(x₀_i) с прямой x_i = x₀_i (точки A и B) определяют существование предельного цикла. Если указанная кривая и прямая не пересекаются, то автоколебания невозможны, а если касаются, то имеет место один предельный цикл.

<16 17 181920 21 22 >

Дата добавления: 2015-06-01; просмотров: 8163;