Статистическая линеаризация нелинейных характеристик

Анализ и синтез нелинейных систем, работающих под воздействием случайных сигналов, значительно усложняется по сравнению с линеаризованной системой, так как, во-первых, закон распределения случайного процесса изменяется за счет изменения коэффициента усиления нелинейного элемента в зависимости от величины входного сигнала, во-вторых, если вместе с полезным сигналом на вход системы поступает случайная помеха, то при прохождении через нелинейный элемент соотношение между ними изменяется.

Для нелинейных элементов нет простой связи между средними значениями, корреляционными функциями и спектральными плотностями случайных сигналов на его выходе и входе. Однако такую зависимость можно формально получить, если заменить нелинейное преобразование случайного сигнала некоторым эквивалентным линеаризованным преобразованием.

Оценить статистические характеристики нелинейных систем позволяет метод статистической линеаризации [2, 9, 10], основанный на замене нелинейной характеристики статистически равноценной линейной. Критериями статистической равноценности служат два принципа:

принцип равенства средних значений и дисперсий случайных процессов на выходе нелинейного элемента и эквивалентного ему линеаризованного элемента;

принцип минимума средней квадратической ошибки, обусловленной заменой нелинейного элемента приближенным линеаризованным элементом.

Заменим нелинейную характеристику элемента

y_н = F(x) (2.74)

линейной зависимостью

y = k´x, (2.75)

которая имеет такие же математическое ожидание и дисперсию на выходе. С этой целью запишем (2.75) в виде

y = k₀ m_x + k₁₁ x^o, (2.76)

где x^o - центрированная случайная функция.

Выберем коэффициенты k₀ и k₁₁ так, чтобы

m_y = k₀ m_x = m_yн ; 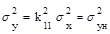, (2.77)

где m_x, m_yн, m_y, 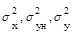- математические ожидания и дисперсии сигналов.

Из выражения (2.77) следует, что для статистической равноценности, исходя из равенства средних значений и дисперсий случайных процессов на выходе нелинейного элемента и эквивалентного ему линеаризованного звена, требуется

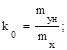(2.78)

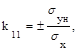(2.79)

причем знак k₁₁ должен совпадать со знаком производной нелинейной характеристики F(x).

Величины k₀ и k₁₁ называются коэффициентами статистической линеаризации. Для их вычисления требуется знать математическое ожидание и дисперсию сигнала на выходе нелинейного элемента:

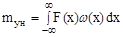; (2.80)

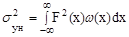, (2.81)

где w(x) - плотность вероятности распределения случайного сигнала на входе нелинейного элемента.

Далее найдем коэффициенты статистической линеаризации на основании второго принципа, обеспечивающего наилучшее приближение корреляционной функции сигнала на выходе нелинейного элемента к корреляционной функции сигнала на выходе линейного звена. Среднее значение квадрата ошибки, обусловленное заменой нелинейного элемента приближенным линеаризованным звеном, исходя из (2.74) и (2.76) определяется выражением

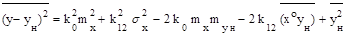(2.82)

и должно быть минимальным. Приравняв нулю производные от последнего выражения по k₀ и k₁₂ , запишем уравнения

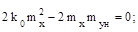(2.83)

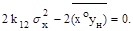(2.84)

Следовательно, в этом случае коэффициенты статистической линеаризации вычисляются по формулам

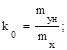(2.85)

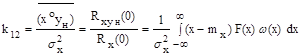. (2.86)

Таким образом, статистическая линеаризация из условия минимумасредней квадратической ошибки дает то же значение коэффициента k₀ , которое было найдено при первом способе линеаризации; коэффициент линеаризации относительно случайной составляющей k₁₂ другой. Рекомендуется брать их среднее арифметическое значение:

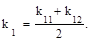(2.87)

Коэффициенты статистической линеаризации зависят не только от характеристик нелинейного элемента, но и от математического ожидания и дисперсии сигнала на его входе. Кроме того, для их вычисления требуется знать закон распределения случайного процесса. При прохождении случайного сигнала через замкнутую систему инерционные звенья линейной части системы приближают закон распределения к нормальному, поэтому для типовых нелинейных характеристик коэффициенты k₀ и k₁ могут быть заранее вычислены.

В заключение следует отметить, что метод статистической линеаризации применим к системам, в которых невозможны автоколебания. Для исследования нелинейных систем с автоколебаниями используется метод совместной статистической и гармонической линеаризации.

Таблицы коэффициентов статистической и совместной статистической и гармонической линеаризации для различных нелинейностей приведены в литературе [17].

ВОПРОСЫ К РАЗДЕЛУ 2

1. Сформулируйте определение и приведите классификацию нелинейных систем. Перечислите особенности нелинейных систем.

2. Каковы основные методы исследования и расчета нелинейных систем, применяемые в инженерной практике?

3. Расскажите о прямом методе Ляпунова.

4. Объясните определение абсолютной устойчивости нелинейных систем по методу В.М.Попова.

5. В чем сущность метода гармонической линеаризации нелинейных характеристик?

6. Поясните исследование нелинейных систем на фазовой плоскости.

7. Какие средства применяются для коррекции нелинейных систем?

8. Что означает вибрационная компенсация нелинейностей?

9. В каких случаях в нелинейной системе возникает скользящий режим? Как построить систему оптимальную по быстродействию?

10.Что такое статистическая линеаризация нелинейных характеристик? Как она осуществляется?