Система линейных дифференциальных уравнений первого порядка. ФСР однородной системы. Общее решение однородной системы.
Определение. Уравнение вида y'+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Пример. Найти общее решение уравнения y'+3y=e2x и частное решение,удовлетворяющее начальным условиям х=0, у=1.
Решение. Данное уравнение является линейным.
Здесь ρ(x)=3 и f(x)=e2x.
Решение ищем в виде y=U∙υ, где U и υ – некоторые функции от х. Находим y'= U'υ+ Uυ' и подставляем в уравнение значение y и y', получаем: U'υ+Uυ'+3Uυ=e2 x или U'υ+U(υ'+3υ)= e2x.
Найдем одно значение υ, при котором выражение в скобках, обращается в нуль: υ'+3υ=0. Получим уравнение с разделяющимися переменными. Решая его получаем: 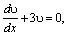
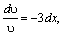 ln υ =–3x,υ=e–3x.
ln υ =–3x,υ=e–3x.
Подставляем найденное значение υ в исходное дифференциальное уравнение, получаем уравнение с разделяющимися переменными:
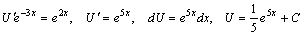 .
.
Итак, общее решение данного уравнения имеет вид:
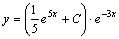 .
.
Найдем частное решение. Для этого подставим начальные условия в выражение для общего решения и найдем С.
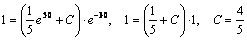 .
.
Частное решение имеет вид: 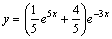
Линейное однородное ОДУ: 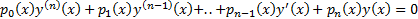 .
.
Теорема о структуре общего решения линейного однородного уравнения:
Если все коэффициенты уравнения линейного однородного дифференциального уравнения непрерывны на отрезке [a;b] , а функции y1(x), y2(x),..., yn(x) линейно независимые решения этого уравнения, то общее решение уравнения имеет вид
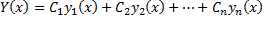 ,
,
где C1,...,Cn — произвольные постоянные.
Фундаментальная система решений нормальной системы однородных линейных ОДУ с постоянными коэффициентами в случае простых действительных корней характеристического уравнения.
Нормальная линейная однородная система n порядка с постоянными коэффициентами - 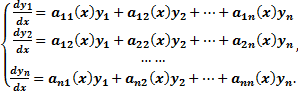 или
или 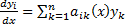 ,
, 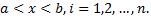 Коэффициенты линейных комбинаций искомых функций постоянны. Эта система в матричной форме
Коэффициенты линейных комбинаций искомых функций постоянны. Эта система в матричной форме 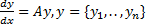 –матричная форма, где A-постоянная матрица. Матричный метод: Из характеристического уравнения
–матричная форма, где A-постоянная матрица. Матричный метод: Из характеристического уравнения 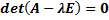 найдем различные корни
найдем различные корни 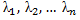 и для каждого корня
и для каждого корня 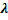 (с учетом его кратности) определим соответствующее ему частное решение
(с учетом его кратности) определим соответствующее ему частное решение 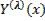 . Общее решение имеет вид:
. Общее решение имеет вид: 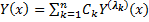 . При этом 1) если
. При этом 1) если 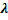 - действительный корень кратности 1, то
- действительный корень кратности 1, то 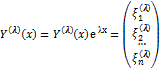 , где
, где 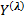 -собственный вектор матрицы А, соответствующий собственному значению
-собственный вектор матрицы А, соответствующий собственному значению 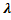 , то есть
, то есть 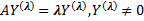 . 2)
. 2) 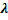 – корень кратности
– корень кратности 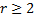 , то соответствующее этому корню решение системы ищут в виде вектора
, то соответствующее этому корню решение системы ищут в виде вектора 
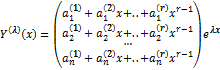 (**), коэффициенты которого
(**), коэффициенты которого 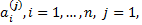 определяются из системы линейных уравнений, получающихся приравнивание коэффициентов при одинаковых степенях x в результате подстановки вектора (**) в исходную систему.
определяются из системы линейных уравнений, получающихся приравнивание коэффициентов при одинаковых степенях x в результате подстановки вектора (**) в исходную систему.
Фундаментальной системой решений НЛОС называется совокупность произвольных n линейно независимых решений 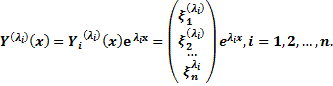
Дата добавления: 2015-05-16; просмотров: 1703;
