Интегрирование линейных ОДУ первого порядка и уравнения Бернулли.
ДУ первого порядка называется линейным, если неизвестная функция y(x) и её производная y’(x) входят в уравнение в первой степени: 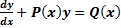 . P(x), Q(x) – непрерывные функции. Уравнение однородное, если Q(x)=0.
. P(x), Q(x) – непрерывные функции. Уравнение однородное, если Q(x)=0.
Форма вариации производной постоянной: 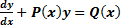 (1), обнуляем правую часть
(1), обнуляем правую часть 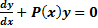
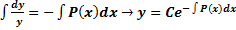 . Общее решение уравнения:
. Общее решение уравнения: 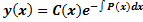 . Находим производную
. Находим производную 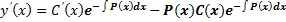 . Подставим y и y’ в уравнение (1):
. Подставим y и y’ в уравнение (1):
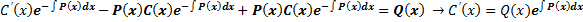
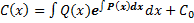 , :
, : 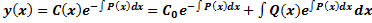 .
.
Уравнения Бернулли имеют следующий вид: 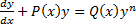
Принцип решения:
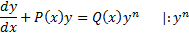
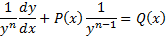
Если обозначить 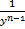 за Z(x), то
за Z(x), то 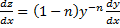 . Отсюда
. Отсюда 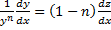 . Подставим это выражение выше и получим:
. Подставим это выражение выше и получим: 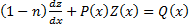
Получили дифференциальное линейное уравнение, принцип решения которого рассмотрен выше.
Пример: 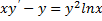 ,
, 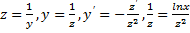 ,
, 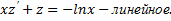
Дата добавления: 2015-05-16; просмотров: 1325;
