Аппроксимация уравнения параболического типа

Решение двухмерной задачи с уравнением параболического типа (6.66) выполняется с помощью сетки аналогичной приведенной на рис. 6.6.

Рассмотрим процесс теплопередачи по длинному однородному стерж­ню длиной L, ось которого совпадает с осью х. Предположим, что в исходном состоянии стержень по всей длине имеет температуру Т = Т₀. Затем, начиная с момента времени t = 0 температура на его правом конце х = L скачком возрастает до T_L, в то время как на левом конце х = 0 поддер­живается температура Т = Т₀. Теплопередачей через боковую поверхность стержня будем пренебрегать.

Учитывая, что в стержне отсутствуют источники тепла (Q = 0), запи­шем в конечных разностях уравнение, эквивалентное (6.66):

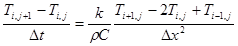(6.80)

или

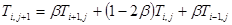(6.81)

где 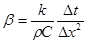. Из (6.80) и (6.81) видно, что шаблон для уравнения пара­болического типа напоминает перевернутую букву Т.

Граничные условия по координате x в данной задаче включают темпе­ратуру на концах стержня: T_1j = 0 при x = 0 и T_nj = T_L при x = L. По времени t начальное условие задает исходное распределение температуры в стержне T(x,t=0) = T₀.

Запишем уравнение (6.81) для каждого узла сетки и, подставляя в него вместо i и j соответствующие этим узлам номера, получим систему связан­ных уравнений.

Решение системы уравнений для данной задачи, так же как и в преды­дущем случае вычисляется с использованием явной схемы.

При этом расчет упрощается за счет того, что распределение темпера­туры в стержне для каждого последующего временного слоя j+1 определяет­ся из известного распределения только в одном предыдущем слое j.

При решении уравнения параболического типа также важен выбор ша­га 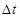. Для обеспечения сходимости и устойчивости метода желательно, что­бы параметр 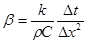в (6.81) не превышал 0,5. Нарушение этого условия приводит к расходящемуся или колеблющемуся решению.