Погрешность решения

Погрешность решения методом конечных разностей в первую очередь определяется ошибкой, вносимой при замене исходного дифференциального уравнения на его конечно-разностный аналог.

Вначале оценим погрешность аппроксимации (6.70) для первой производ­ной, используя разложение u(x) в окрестностях точки x_i в ряд Тейлора:

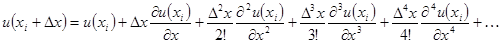(6.82)

откуда

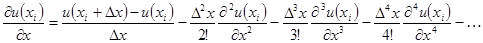(6.83)

Согласно (6.82) погрешность конечно-разностной аппроксимация по формуле (6.70) обусловлена тем, что в ней не учитываются слагаемые высоких порядков, начиная с 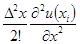. Можно утверждать, что в (6.83) слагае­мые убывают по мере увеличения их порядка. Поэтому ошибка (6.70) приближенно равна .

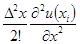Аналогичную оценку нетрудно провести и для второй производной. Для этого необходимо воспользоваться (6.82) и аналогичным разложением, за­писанным для :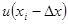

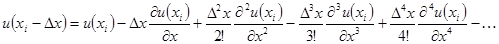(6.84)

Сложив (6.82) и (6.84) получим выражение для второй производной:

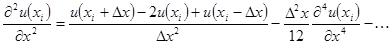(6.85)

Из сравнения (6.85) и (6.72) видно, что погрешность (8) определяется не уч­тенными в ней слагаемыми высоких порядков, начиная с 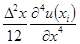. Поэтому ошибка (6.72) уменьшается пропорционально квадрату 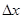. Данный ре­зультат полезно учитывать при выборе шага сетки. Так, например, уменьшение вдвое шага 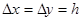приводит к снижению ошибки аппроксимации для уравнения эллиптического типа в четыре раза.

Нельзя утверждать, что уменьшение шага сетки однозначно повышает точность решения методом конечных разностей. С увеличением количества уз­лов сетки возрастает объем вычислений и, следовательно, растут вычислитель­ные погрешности. На практике для оценки погрешности решения можно про­вести ряд пробных расчетов с разными значениями шага сетки и выбрать вари­ант, обеспечивающий приемлемую точность при невысоких вычислительных затратах.

Существуют различные формулировки метода конечных элементов, различающиеся как в основных, так и в менее значительных деталях. Огра­ничимся кратким рассмотрением основных этапов решения задачи этим ме­тодом.