Элементы математической статистики

Результаты наблюдений во многих случаях можно представить последовательностью действительных чисел .

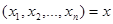Для того, чтобы из ряда наблюдений можно было извлечь полезную информацию, необходимо иметь модель явления. Вероятностные модели оказываются наиболее пригодными при анализе явлений, исходы 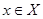которых обладают некоторой степенью неопределенности. Понятие неопределенности в теории вероятностей формализуется путем введения распределения вероятностей на множестве 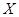. В простейшем случае, когда 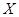конечное или счетное множество, задаются вероятности 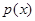всех его элементов 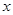, так что 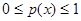и .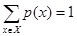

Любое множество 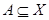называют в этом случае событием, а его вероятность определяют формулой .

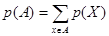Взаимоотношение явления и его вероятностной модели имеет статистический характер, то есть обнаруживается при повторных наблюдениях за явлением. Частоты исходов в длинном ряду испытаний стабилизируются, их колебания с ростом числа испытаний уменьшаются. Это эмпирический факт, называемый законом устойчивости частот, наблюдается в самых различных ситуациях. Уже выходя за пределы реального опыта, полагают, что при неограниченном повторении частоты стремятся к пределам, которые и принимают за вероятности соответствующих исходов или событий.

Генеральная совокупность. Выборка. Статистические ряды

Пусть задача состоит в том, чтобы исследовать заданный качественный или количественный признак, характеризующий элементы некоторой последовательности (совокупности) наблюдений. Все множество объектов, входящих в рассматриваемую совокупность называют генеральной совокупностью. Число элементов генеральной совокупности может быть достаточно большим (в теоретических рассмотрениях используется и совокупности, содержащие бесконечное множество элементов).

Часть генеральной совокупности, выбранную из нее некоторым (случайным) образом, называют выборочной совокупностью (выборкой). Объем выборки, обозначаемый 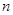(по количеству элементов), может быть и сравнительно большим и малым, но не может содержать меньше двух единиц. Выборочный метод является основным при изучении статистических совокупностей. Его преимущество перед сплошным учетом всех членов генеральной совокупности заключается в том, что он сокращает время и затраты труда (за счет уменьшения числа наблюдений), а главное позволяет получать информацию о таких совокупностях, сплошное исследование которых практически невозможно или нецелесообразно.

Элементы совокупности называют вариантами. Существует два основных способа отбора вариант из генеральной совокупности: повторный и бесповторный. В практике обычно применяют бесповторный отбор.

Статистическими рядами называют ряды числовых значений некоторого признака, расположенного в определенном порядке.

Расположим варианты 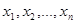( 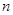‑ объем выборки) в порядке возрастания и перенумеруем их заново: 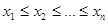, где

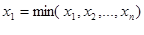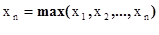, . (6.88)

Такую перенумерованную последовательность часто называют вариационным рядом.

Числа, показывающие сколько раз отдельные варианты встречаются в данной совокупности, называются частотами или весами вариант и обозначаются 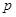или .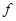

Общая сумма частот всегда равна объему выборки. Говорят еще об относительных частотах (выражаются в частях или % от ).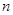

Интервальный вариационный ряд, такой статистический ряд, в котором частоты распределяются по отдельным интервалам или промежуткам (от ‑ до), на которые разбивается вариация признака в пределах от минимальной до максимальной варианты совокупности. Эти промежутки или классовые интервалы могут быть равными и неравными по ширине. Чаще всего рассматриваются равные интервалы. Величина равных интервалов определяется делением размаха варьирования признака ( 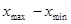) на число групп или классов ( 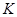), намечаемых при построении вариационного ряда:

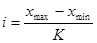, (6.89)

где 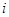‑ величина классового интервала, а величина 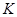определяется по формуле Стерджеса .

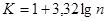В общем случае техника построения вариационного ряда сводится к следующему:

1. Составляем сводку исходных данных.

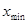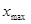2. Отыскиваем и варианты.

3. Определяем величину классового интервала 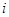по формуле данной выше. Если значения признака выражены целыми числами и классовый интервал 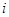окажется равным 1 (или »1), выборка распределяется в безинтервальный вариационный ряд. Если 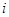¹1, выборку следует распределять в интервальный вариационный ряд. Кроме того, следует соблюдать правило, согласно которому величина классового интервала должна соответствовать точности, принятой при измерении учитываемого признака (если e=0,001 , то классовый интервал тоже определяется с точностью 0,001).

4. При построении интервального вариационного ряда следует добиваться того, чтобы минимальная варианта 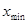попадала в середину классового интервала, то есть, 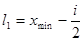, где 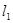- нижняя граница первого классового интервала. Определяем верхнюю границу первого классового интервала 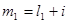, второго классового интервала 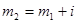, 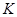- того классового интервала .

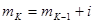5. Наметив классовые интервалы, остается распределить по ним варианты выборки, то есть, определить частоты каждого класса.