Формирование сетки
Метод конечных элементов основывается на том, что любое непрерывное распределение физической переменной u(x,y,z,t) в расчетной области, например деформацию или температурное поле, можно аппроксимировать набором кусочно-непрерывных функций, определенных на конечном числе подобластей (конечных элементов). Данные элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.
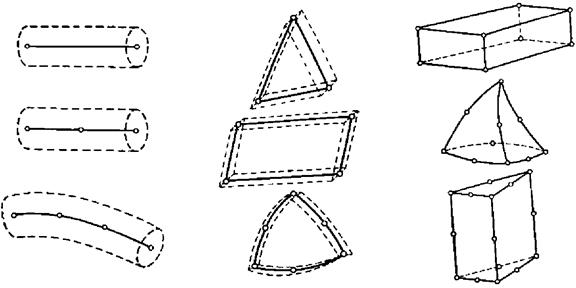
В зависимости от геометрии и размерности задачи используют различные виды конечных элементов (см. рис. 6.7). Чаще всего применяются простейшие элементы - симплексы.
а б в
Рис. 6.7 ‑ Некоторые виды конечных элементов: a - одномерные; б -двухмерные; в - трехмерные
Количество узлов в симплексе на единицу превышает размерность задачи. Для двухмерной задачи симплекс-элементом будет являться прямолинейный трехузловой треугольник, а для трехмерных - прямолинейный четы-рехузловой тетраэдр. Широкое применение симплексов обусловлено тем, что они позволяют заполнять расчетную область произвольной формы полностью без разрывов, а также на них удобно использовать в качестве аппроксимирующих функций линейные полиномы.
Обычно для разбиения расчетной области на элементы используется специальный алгоритм покрытия, обеспечивающий автоматическую генерацию сетки.
Одна из таких процедур работает следующим образом (см. рис. 6.8, а). Вначале производится нанесение с некоторым шагом узлов на границу области. После этого внутри области строится вспомогательная кривая эквидистантная границе. На кривую также наносятся узлы. Поочередное соединение узлов на первом и втором контурах дает симплексы. Далее все операции повторяются до заполнения симплексами всей области.
Известны и другие алгоритмы формирования конечных элементов, например, «картографический», использующий наложение на расчетную область сетки, которая затем адаптируется к границам и неоднородностям геометрии, или методы, основанные на заполнении объекта набором фигур (тел) с использованием свойств симметрии или отражения.
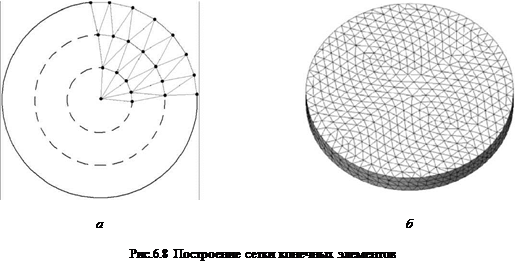 |
Пример автоматически сгенерированной трехмерной сетки для круглого диска показан на рис. 6.8, б.
Конечно-элементная аппроксимация
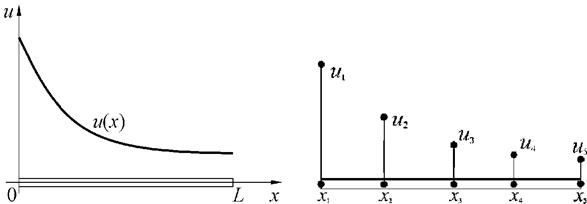
Рассмотрим построение аппроксимации на одномерном примере. Пусть требуется найти распределение некоторой непрерывной функции u(x) вдоль стержня (см. рис. 6.9, а). На практике эта функция может описывать, например, распределение температуры или деформацию стержня.
а б
Рис. 6.9 ‑ Одномерное распределение
Выберем и пронумеруем ряд точек вдоль оси х ‑ это узловые точки (рис. 6.9, б). В нашем примере взято всего пять точек. Вообще говоря, их может быть произвольное количество, и располагаться они могут не на равном расстоянии друг от друга. Предположим, что значения в узловых точках известны. Они обозначены на рис. 6.9, б в соответствии с номерами узлов – u1 u2, u3, u4,.
Разбиение расчетной области, то есть стержня, на конечные элементы может быть проведено различными способами. Можно, например, выделить четыре элемента, включив в каждый из них по два соседних узла (рис. 6.10 а). А можно выделить в стержне всего два элемента, содержащие по три узла (рис. 6.10, б).
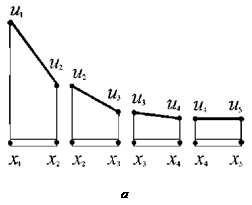 | 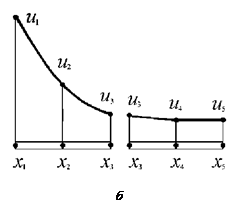 | ||
Рис. 6.10 ‑ Варианты разбиения стержня на элементы
При использовании четырех элементов, каждый из которых включает только два узла, аппроксимирующая функция в пределах элемента будет линейна по х, так как две точки однозначно определяют прямую линию. Общая аппроксимация зависимости и(х) по всей длине стержня будет складываться из четырех отрезков прямых (рис. 6.10, а).
Зависимость u(x) в пределах одного элемента, ограниченного двумя соседними узлами xi и Xj? (j = i + 1), можно представить линейным интерполяционным полиномом u(x) ~ ? а + ax x. Определив параметры а и ах по известным в точках xi и xj ? значениям функции ui и Uj,? запишем интерполяционный полином, то есть функцию элемента следующим образом:
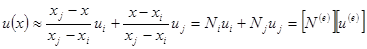 (6.86)
(6.86)
где Ni и Nj - функции формы конечного элемента, ui и uj - значения функции u(x) в точках xi и xj, 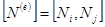 – матричная строка функций формы элемента
– матричная строка функций формы элемента
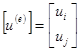
Следует отметить, что ряд терминов метода конечных элементов получили название из механики, где он впервые начал активно использоваться.
В случае разбиения области на два элемента (рис. 6.10, б) три узловые точки в каждом из них позволяют однозначно определить функции элементов в виде полиномов второй степени. Соответственно распределение u(х) на всей длине стержня будет аппроксимироваться кусочно-непрерывной квадратичной функцией. При этом общая аппроксимация для стержня может содержать излом из-за несовпадения углов наклона графиков полиномов (их первых производных) в третьем узле.
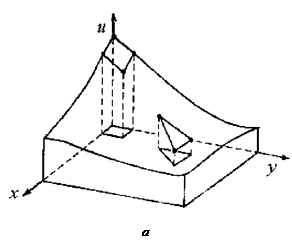
Для двухмерной или трехмерной задачи аппроксимация строится аналогичным образом. В зависимости от вида элементов (количества используемых в них узлов) также применяется линейная или нелинейная аппроксимация. Примеры аппроксимации двухмерной непрерывной функции u(x,y) приведены на рис. 6.11.
 | |||
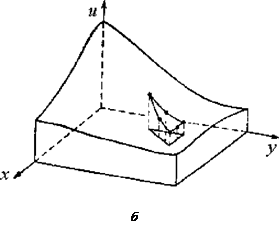 | |||
Рис. 6.11 ‑ Моделирование двухмерной скалярной функции с помощью линейной (а) и нелинейной (б) аппроксимации
Функция формы элемента будет представлена плоскостью, если для него взято минимальное число узлов, которое для треугольного элемента равно трем, а для четырехугольного ‑ четырем. В этом случае используют линейную аппроксимацию 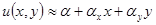 .
.
По аналогии с одномерным случаем линейный интерполяционный многочлен для простейшего треугольного элемента, включающего только три узла, записывают в виде
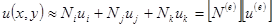 (6.87)
(6.87)
где Nt , Nj , Nk - функции формы элемента, и ,?uj , uk - значения функции в узлах, принадлежащих элементу, [N(e)] - матричная строка функций формы элемента, [u(e)] - вектор-столбец значений функции u(x,y) в его узлах. Если элемент содержит большее количество узлов, то аппроксимирующая функция элемента будет отображаться криволинейной поверхностью.
Для всей расчетной области аппроксимацией распределения u(x,y) является кусочно-линейная (или кусочно-нелинейная) поверхность, каждый из участков которой определяется на отдельном элементе с помощью значений u(x,y) в принадлежащих ему узлах.
Для построения аппроксимации так, как это было показано выше, необходимо знать распределение u(x,y) во всей расчетной области. Однако до решения задачи эта зависимость обычно как раз и не известна. Тем не менее, используя аппроксимирующие формулы (6.86) или (6.87), решение можно получить. Способы отыскания решения рассмотрены ниже.
Построение решения
Вначале необходимо провести объединение конечных элементов в ансамбль. Значения u1, u2, и3, ... в узлах теперь будем рассматривать как неизвестные переменные, которые необходимо найти. Сформируем из этих значений, взятых по всей расчетной области, столбцовую матрицу, которую обозначим 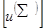 . Каждой строке
. Каждой строке 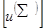 соответствует узел сетки конечных элементов. Тогда аппроксимацией для всей расчетной области (в двухмерном случае) будет
соответствует узел сетки конечных элементов. Тогда аппроксимацией для всей расчетной области (в двухмерном случае) будет
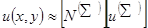 ,
,
где 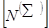 - матричная строка функций формы всех конечных элементов, входящих в расчетную область. При составлении матриц
- матричная строка функций формы всех конечных элементов, входящих в расчетную область. При составлении матриц 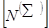 и
и 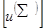 производится сквозная нумерация узлов. Для двух- и трехмерных задач эта процедура сложна и от нее в значительной степени зависит время расчета.
производится сквозная нумерация узлов. Для двух- и трехмерных задач эта процедура сложна и от нее в значительной степени зависит время расчета.
Следующий этап ‑ построение разрешающей системы алгебраических уравнений на основе конечно-элементной аппроксимации. В результате решения задачи узловые значения u1, u2, u3, ... должны быть «подобраны» так, чтобы они обеспечивали наилучшее приближение к истинному распределению u(x,y). Этот «подбор» может осуществляться различными способами.
Существуют вариационная и проекционная формулировки метода конечных элементов. При вариационном подходе производится минимизация некоторого функционала, связанного с исходным дифференциальным уравнением. Например, в задачах механики может минимизироваться потенциальная энергия системы. Процесс минимизации приводит к решению системы алгебраических уравнений относительно узловых значений и(х).
Проекционный вариант метода конечных элементов является частным случаем метода взвешенных невязок. Последний основан на минимизации невязки в дифференциальном уравнении при подстановке в него приближенного решения вместо точного. В методе конечных элементов оценка невязки производится по отдельным элементам и также сводится к решению системы алгебраических уравнений относительно узловых значений и(х).
При построении решения функции формы N позволяют определять в пределах каждого элемента пространственные дифференциальные операторы первого порядка от скалярного или векторного поля (см. (22)).
В методе конечных элементов также как и в методе конечных разностей матрица коэффициентов системы уравнений включает большое число нулевых элементов, что облегчает решение задачи.
К достоинствам метода конечных элементов, благодаря которым он находит широкое применение, относятся гибкость и разнообразие сеток, четко формализованные алгоритмы построения дискретных задач для произвольных областей, простота учета естественных краевых условий. Кроме того, этот метод применим к широкому классу исходных задач, а оценки погрешностей приближенных решений, как правило, получаются при менее жестких ограничениях, чем в методе конечных разностей.
Несмотря на то, что метод конечных разностей на первый взгляд представляется наиболее легким в реализации, и был разработан раньше метода конечных элементов, последний в настоящее время является доминирующим в современных расчетных программах.
Дата добавления: 2015-04-03; просмотров: 2066;
