Аппроксимация уравнения гиперболического типа

Построение алгебраических уравнений на основе дифференциального уравнения гиперболического типа (1) выполняется, так же как и в предыду­щем случае, заменой производных конечно-разностными аналогами. В качестве примера рассмотрим задачу про­дольных колебаниях тонкого однородного стержня длиной L, когда его дефор­мация u зависит только от продольной (вдоль оси стержня) координаты х и времени t.

Колебания стержня описываются дифференциальным уравнением

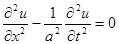(6.75)

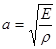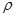где , E и - модуль упругости и плотность материала стержня.

Аппроксимация уравнения производится на сетке в координатах t и х. Примерный вид сетки показан на рис. 6.6. Данная задача не имеет верхней гра­ницы по координате t. Это объясняется тем, что с формальной точки зрения колебания в стержне могут продолжаться неопределенно долгое время, даже если будут учтены потери, приводящие к их затуханию.

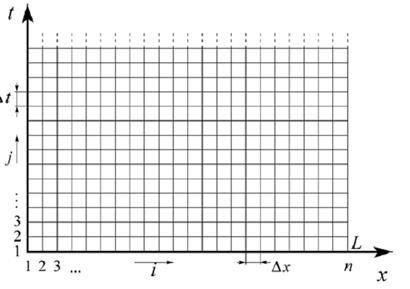
Рис. 6.6 ‑ Сетка в координатах t и x

Используя сетку, запишем в конечных разностях уравнение, эквива­лентное (6.75):

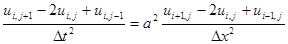(6.76)

или

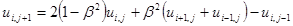(6.77)

где 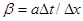. Из (6.76) и (6.77) видно, что форма шаблона уравнения гипербо­лического типа подобна форме шаблона ура внения эллиптического типа.

Аналогично предыдущей задаче запишем уравнение (6.77) для каждого узла сетки и, подставляя в него вместо i и j соответствующие этим узлам но­мера, получим систему связанных алгебраических уравнений.

В качестве граничных условий по x в данной задаче могут использо­ваться любые условия, описывающие способ закрепления стержня. Например, жесткое закрепление предполагает нулевой сдвиг на концах стержня. Это соответствует условию u(x=0,t) = 0 и u(x=L,t) = 0, где x = 0 и x = L - координаты концов стержня.

По времени t в качестве начальных условий зададим при t = 0 исходную деформацию стержня и начальную скорость его колебаний

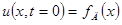(6.78)

Решение системы уравнений для рассматриваемой задачи можно полу­чить с помощью сравнительно простой процедуры, называемой явной схемой. Эта схема строится на том, что все уравнения системы последовательно свя­заны между собой.

Расчет будем проводить в следующем порядке. Вначале определим де­формацию стержня в моменты t = 0 и 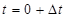. Для t = 0 деформация 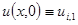известна из заданных начальных условий (6.78). Для следующего момента времени 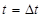деформацию 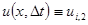определим с помощью вто­рого начального условия, задающего скорость 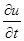при t = 0:

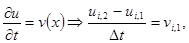тогда (6.79)

При известных из (6.78) и (6.79) u_i,1 и u_i,2 начнем решение задачи следую­щим образом. Полагая, что j = 2, то есть u_i,j-1 = u_i,1 и u_t,j = u_i,2, подставим в (6.77) известную из (6.78) соответствующую t = 0 начальную де­формацию 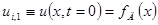, и соответствующую 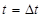деформацию (см. (6.78)). Вычисление правой части (6.77) позволяет опреде­лить 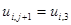в момент времени .

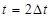Далее действуя аналогично и сдвигая шаблон решения на одну линию сетки по координате t, вычисляются последовательно фазы колебаний u_i,4 - из u_i,2 и u_i,3, затем u_i,5 - из u_i,3 и u_i,4 и так далее. То есть очередной временной слой j+1 рассчитывается из предыдущих с индексами j и j-1.

При решении гиперболического уравнения следует обращать внимание на выбор шага сетки по x и t. Теоретически можно показать, что приближен­ное решение, получаемое с помощью (6.77), сходится к точному пр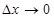и и 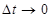со скоростью 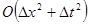если 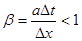. Иначе говоря, если вы­бран шаг сетки 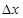по координате x, то появляется ограничение на шаг по времени 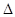t.

При 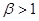метод становится неустойчивым как в абсолютном, так и в относительном смысле. Последнее означает, что по мере продолжения вы­числений ошибки катастрофически нарастают. Теоретически показано, что при в = 1 метод устойчив и конечно-разностное решение совпадает с точным. При 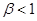решение хотя и устойчиво, но его точность с уменьшени­ем 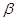убывает.