Классификация уравнений по математической форме

Во многих случаях для описания физических процессов используют уравнений с частными производными до второго порядка включительно.

Так, например, изучение свободных колебаний различной природы приводит к волновым уравнениям вида

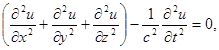(6.65)

где u(x,y,z,t) - функция, описывающая волновой процесс, x, у, z - координаты, с - скорость распространения волны в данной среде, t - время. Оператор 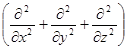принято обозначать значком 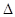, который в этом случае носит название оператора Лапласа.

Процессы распространения тепловой энергии описываются уравнением теплопроводности

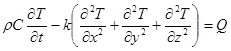(6.66)

где р и C ‑ плотность и теплоемкость вещества, Т - температура, к - коэффициент теплопроводности, Q ‑ плотность источников тепла.

Анализ стационарных состояний, например, статических тепловых, электрических, магнитных полей или деформаций при статических нагруз­ках проводят, используя уравнение Пуассона

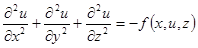(6.67)

где u(x,y,z) ‑ функция, описывающая статическое поле, /x,y,z) - распреде­ленные источники. Если (x,y,z) = 0, то (6.67) обращается в уравнение Лапласа:

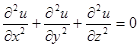(6.68)

Известны и другие виды задач и соответствующие им дифференциаль­ные уравнения в частных производных, например, уравнение диффузии или уравнение Гельмгольца.

Несмотря на различие процессов, описываемых рассмотренными урав­нениями, и форм их записи, все они с математической точки зрения могут быть представлены как частные случаи обобщенной формы дифференциаль­ного уравнения второго порядка.

Рассмотрим уравнение второго порядка с двумя независимыми пере­менными x и y:

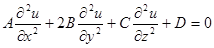(6.69)

где A, B, С и D ‑ некоторые функции, зависящие в общем случае от х, у, u, ди/дх и ди/ду, причем A, B и С одновременно не обращаются в ноль. Диффе­ренциальные уравнения, описывающие физические поля, могут быть нели­нейными. Однако на практике многие задачи рассматриваются в линейном приближении, когда уравнение с частными производными линейно относи­тельно неизвестной функции и и ее частных производных.

На основании того, что уравнению (6.69) можно поставить в соответствие квадратичную форму 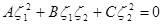, по математической природе различают следующие типы квазилинейных уравнений:

1) гиперболический, если B² ‑ 4AC>0 ‑ его аналогом является волно­вое уравнение (6.65);

2) параболический, если B² ‑ 4AC = 0 ‑ его аналог уравнение тепло­проводности (6.66);

3) эллиптический, если B² ‑ 4AC < 0 ‑ аналог уравнение Пуассона (6.67) или Лапласа (6.68).

В задачах, описываемых дифференциальными уравнениями в частных производных, другой важной составляющей помимо самого уравнения явля­ется формулировка дополнительных условий.

Для задач с уравнениями гиперболического или параболического типа, содержащих в качестве независимой переменной время t, условия по t обычно формулируются как начальные, описывающие исходное состояние системы. По координатам х, у и z задают граничные условия. В тепловых зада­чах они, например, описывают распределение температуры на границе расчетной области. В задачах с уравнениями эллиптического типа, не содержа­щими переменную t, используют только граничные условия по координатам х, у и z, а саму задачу называют краевой.

Если краевое условие задает распределение функции u на границе, то его принято называть условием Дирихле. Условие, определяющее производ­ную 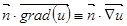на границе расчетной области, называют условием Неймана. Здесь 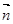‑ единичная нормаль к границе. Условия, представляющие собой комбинацию двух вышеназванных, называют смешанными.

С помощью дифференциальных уравнений формулируют и другой вид задач - задачи на собственные значения, связанные, например, с определени­ем собственных волн (частот) колебательных систем или волноведущих структур. Однако здесь они не рассматривается.

Приведенная классификация позволяет определить общие подходы к решению дифференциальных уравнений в задачах различных по физической сути, но сходных с математической точки зрения. В настоящее время широ­кое распространение получили метод конечных разностей и метод конеч­ных элементов, основы которых и будут рассмотрены ниже.

Метод конечных разностей заключается в том, что дифференциальное уравнение в частных производных заменяется соответствующей ему систе­мой алгебраических уравнений. Решение этой системы дает приближенное решение для искомой функции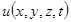

Метод включает следующие основные этапы:

1) построение сетки, охватывающей рассматриваемую область, напри­мер, элемент конструкции какого-нибудь устройства;

2) построение на полученной сетке конечно-разностной аппроксима­ции, эквивалентной исходному дифференциальному уравнению и дополни­тельным условиям;

3) формирование на основе конечно-разностной аппроксимации систе­мы алгебраических уравнений и ее решение.

Рассмотрим перечисленные этапы на примере двухмерных задач.