Построение сетки

Формирование сетки производится с учетом геометрии задачи, напри­мер, формы детали, для которой выполняется расчет. Обычно для деталей, имеющих прямоугольную форму, используют декартову систему координат и соответственно прямоугольную сетку. На рис. 6.4 приведен пример такой двухмерной сетки, нанесенной на прямоугольную пластину.

В методе конечных разностей применяют и другие виды сеток. Напри­мер, если исследуемая конструкция содержит элементы с осевой симметрией, используют полярную сетку.

В дальнейшем решение задачи строят, опираясь на узлы сетки, то есть на точки пересечения ее линий (рис.6.4).

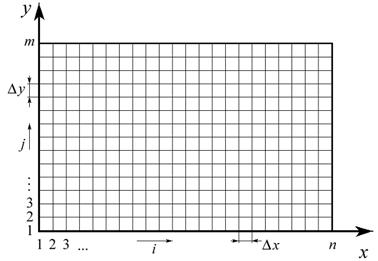
Рис. 6.4 ‑ Прямоугольная сетка

Конечно-разностная аппроксимация производных в дифференциальном уравнении строится путем замены этих производных на их приближенные аналоги с помощью сетки. Так, например, частную производную 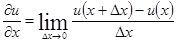в точке (x_i, у_i) можно заменить прибли­женным значением правой производной

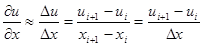(6.70)

или левой производной

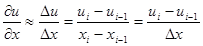(6.71)

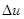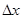где и ‑ приращения функции и аргумента, u_i, x_i и u_i+1, x_i+1 ‑ значения функции и аргумента в узлах i и i+1, причем 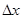‑ шаг сетки по координате х. Аналогично получается формула для второй производной д²u/дx² :

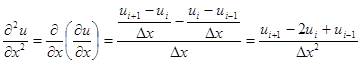(6.72)

В полученных выражениях в отличие от точных производных исполь­зуются малые, но не бесконечно малые разност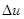и и 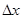. Поэтому сам метод и получил название метода конечных разностей. Формулы для производных по независимым переменным у, z, t получают аналогично.