Метод стрельбы
Итак, если дана краевая задача, например, в вышеприведенной формулировке, то в методе стрельбы она заменяется задачей Коши для того же уравнения (6.60) но с начальными условиями
u(a)=A, 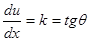 (6.62)
(6.62)
Здесь u(a) ‑ точка, которая является началом кривой решения u(x) дифференциального уравнения, 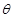 - угол наклона касательной к этой кривой в начальной точке.
- угол наклона касательной к этой кривой в начальной точке.
Считая решение задачи Коши зависящим от начального условия 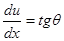 , будем подбирать такое значение
, будем подбирать такое значение 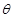 , при котором кривая решения u(x) в точке b даст совпадающий с (6.61) результат u(b) = B. Если это условие будет выполнено, то решение задачи Коши совпадет с решением краевой задачи.
, при котором кривая решения u(x) в точке b даст совпадающий с (6.61) результат u(b) = B. Если это условие будет выполнено, то решение задачи Коши совпадет с решением краевой задачи.
Применительно к описанному подходу называние «метод стрельбы» вполне оправдано, поскольку в нем производится как бы "пристрелка" по углу наклона кривой u(x) в начальной точке.
Чтобы сократить количество попыток при поиске решения u(x), применяют различные стратегии подбора параметра 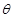 . Например, при использовании метода половинного деления действуют следующим образом. Вначале выполняют два пробных расчета при значениях параметра
. Например, при использовании метода половинного деления действуют следующим образом. Вначале выполняют два пробных расчета при значениях параметра 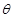 равных
равных 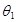 и
и 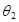 . Эти значения выбирают таким образом, чтобы при
. Эти значения выбирают таким образом, чтобы при 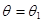 решение давало в точке x = b «перелет», то есть u(b) > B, а при
решение давало в точке x = b «перелет», то есть u(b) > B, а при 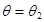 - «недолет», то есть u(b) < B.
- «недолет», то есть u(b) < B.
Далее, используя в начальном условии (6.61) значение 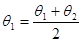 , вновь численно решают задачу Коши. Из трех полученных решений отбрасывают то, которое дает в точке x = b наибольшее отклонение от B. Затем от двух оставшихся значений параметра
, вновь численно решают задачу Коши. Из трех полученных решений отбрасывают то, которое дает в точке x = b наибольшее отклонение от B. Затем от двух оставшихся значений параметра 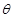 находят среднее
находят среднее 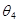 и вновь выполняют с этим значением расчет.
и вновь выполняют с этим значением расчет.
Повторение описанного процесса прекращают, когда разность двух последовательно найденных значений 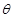 станет меньше некоторого заданного малого числа или достаточно малым будет отклонение u(b) от B. Подобный алгоритм может быть построен и с использованием метода Ньютона.
станет меньше некоторого заданного малого числа или достаточно малым будет отклонение u(b) от B. Подобный алгоритм может быть построен и с использованием метода Ньютона.
Дата добавления: 2015-04-03; просмотров: 1644;
