Погрешность решения и выбор шага

Как было показано выше, порядок точности метода p определяет ошибку дискретизации ~h^р+1. Знание порядка ошибки не обеспечивает ее прямую оценку. Получить такую оценку позволяет правило Рунге (формула двойного пересчета).

Пусть одношаговый метод имеет порядок точности p. Тогда погреш­ность, равная разности точного решения u_T и приближенного 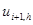, получен­ного численно с использованием шага h, имеет порядок p+1:

где C ‑ константа, не зависящая от h. При расчете с уменьшенным вдвое шагом, равным h/2, погрешность изменится:

Вычитая последнее выражение из предыдущего, определим изменение

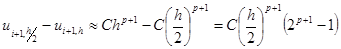
Выражая из последнего соотношения постоянную C и подставляя в преды­дущую формулу, получим оценку погрешности по правилу Рунге

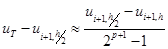(6.57)

Ошибка дискретизации стремится к нулю при стремлении h к нулю. Следовательно, уменьшая шаг h можно сделать локальную ошибку (на шаге) сколь угодно малой. Однако при уменьшении h необходимо увеличить коли­чество шагов. Поэтому сокращение h не приводит к такому же снижению глобальной (накапливаемой от шага к шагу) ошибки.

Малые ошибки, появившиеся в начале вычислений, могут совершенно исказить решение, если только не подобрать подходящий численный метод. Это явление иногда называют «неустойчивостью». Неустойчивость проявля­ется в катастрофическом нарастании погрешности решения вплоть до воз­никновения паразитных осцилляции кривой решения.

На практике уменьшению h препятст­вуют и ошибки округления, вызванные неточ­ностью представления чисел в компьютере. При уменьшении шага, начиная с некоторого h0, вклад ошибок округления преобладает, что приводит к возрастанию погрешности реше­ния.

Обычно алгоритмы обеспечивают автоматический выбор шага. Для этого вы­полняется два пробных расчета - с заданным шагом h и с уменьшенным вдвое h/2.

В простейшем случае ограничиваются сравнением результатов решений в одной и той же точке:

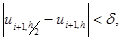
где 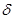‑ некоторое малое положительное число, определяющее требования к точности. Более сложные оценки основываются на формулах подобных правилу Рунге. Если оценка показывает большую ошибку, алгоритм переходит на уменьшенный вдвое шаг.