Метод Адамса

В простейшем случае многошаговый метод опирается только на две последние точки решения - (x_i, u_i) и (x_i, u_i). Вычисление следующей точки строится на двух интервалах ‑ от x_i-1 до x_i и от x_i до x_i+1. В данном случае го­ворят, что метод является двухшаговым.

Для получения расчетной формулы двухшагового метода проинтегри­руем обе части дифференциального уравнения (1) на интервале от x_i до x_i+1. Интегрирование левой части дает

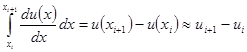(6.58)

Для интегрирования правой части (6.47) заменим f(x, u) = f(x, u(x)) на ин­терполяционный многочлен F(x). Для двух известных точек x_i-1 и x_i может быть построен линейный многочлен, совпадающий с кривой решения в точ­ках (x_i-1,u_i) и (x_i, u_i):

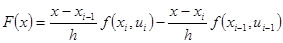
Тогда интегрирование правой части дает

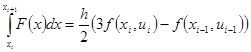(6.59)

Приравнивая правые части (6.58) и (6.59) и применяя сокращенные обозначения f_i=f(x_i,u_i), f_i+1 = f(x_i+1,u_i+1), запишем формулу двухшагового метода

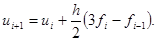
Аналогично, учитывая большее число предыдущих точек решения можно построить формулы экстраполяционного метода Адамса-Башфорта:

Первая соответствует трехшаговому, а вторая - четырехшаговому методу.

Методы прогноза и коррекции (предиктор-корректор)

Аналогичные вышеприведенным выражения можно получить, включая в интерполяционный многочлен рассчитываемую точку x_i+1 как известную. Этот подход дает формулы метода Адамса-Моултона:

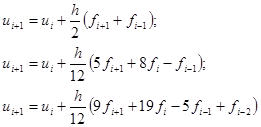
Данный метод является неявным, то есть требует решения уравнения относительно u_i+1, что представляется неудобным. Тем не менее, неявные формулы применяются на практике, так как позволяют повысить устойчи­вость решения и существенно увеличить шаг.

Обычно решение строится в два этапа. Сначала по явной схеме опреде­ляют прогноз u_i+1, например, по формуле Адамса-Башфорта. На втором этапе производится коррекция u_i+1 по неявной формуле. Далее, многократно ис­пользуя неявную формулу, можно дополнительно уточнять u_i+1 подобно то­му, как это делается в методе простой итерации. Однако обычно ограничи­ваются единственной итерацией. Описанный алгоритм многошаговых мето­дов получил название метода прогноза и коррекции.