Краевая задача

В краевой задаче требуется найти решение обыкновенного дифферен­циального уравнения с дополнительными условиями, заданными при не­скольких различных значениях независимой переменной.

Например, для обыкновенного дифференциального уравнения второго порядка

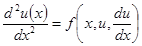(6.60)

эти условия задаются в двух разных точках x = a и x = b:

u(a)= A, и u(b)=B. (6.61)

Поскольку эти точки определяют границы области a<x<b, в которой обычно и отыскивается решение, поставленные в них дополнительные усло­вия называют граничными или краевыми. В инженерной практике, например, такая задача может быть связана с расчетом прогиба стержня при заданном способе закрепления его концов.

Одним из методов решения краевой задачи является метод конечных разностей. Этот метод будет рассмотрен в следующей лабораторной работе. Другим способом решения краевой задачи является ее приведение к задаче Коши путем замены дополнительных условий. Рассмотрим метод стрельбы, использующий этот подход.