Метод стрельбы для линейного дифференциального уравнения

Если обыкновенное дифференциальное уравнение второго порядка яв­ляется линейным, то есть имеет вид

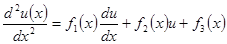(6.63)

при граничных условиях, то поиск решения методом стрельбы сущест­венно упрощается.

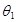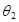Выполнив два «пристрелочных» расчета при и , как это было опи­сано ранее, получим два решения u₁(x) и u₂(x). Если u₁(b) = B₁ и u₂(b) = B₂, причем 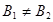, то решением краевой задачи будет линейная комбинация двух решений

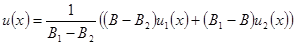(6.64)

Подставляя в это выражение при x = a значения u₁(a) = A и при x = b значения u₁(b) = B₁, u₂(b) = B₂, нетрудно убедиться, что оно удовле­творяет обоим исходным граничным условиям задачи.

Большое число задач, связанных с анализом физических (и не только физических) полей описываются дифференциальными уравнениями в част­ных производных. К сожалению, во многих случаях, представляющих прак­тический интерес, найти аналитическое решение таких задач трудно или практически невозможно. Это обычно обусловлено сложной формой или не­однородностью свойств области, в которой отыскивается решение.

Однако результат можно получить численно с помощью компьютера. Подходы к решению дифференциальных уравнений с частными производ­ными определяются их математической формой. Поэтому рассмотрим клас­сификацию уравнений с этой точки зрения.