Аппроксимация уравнения эллиптического типа
Преобразование уравнения эллиптического типа (3) для двухмерной задачи (когда 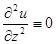 производится путем замены в нем производных
производится путем замены в нем производных 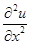 и
и 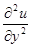 конечно-разностными формулами. Заменив в (6.37)
конечно-разностными формулами. Заменив в (6.37) 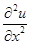 с помощью (6.72) и используя аналогичное выражение для
с помощью (6.72) и используя аналогичное выражение для 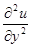 , получим
, получим
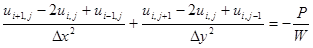 (6.73)
(6.73)
где индексы i и j отсчитываются соответственно по осям X и Y.
Для упрощения анализа предположим, что в сетке используются квадратные ячейки, то есть 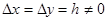 , тогда
, тогда
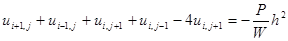 (6.74)
(6.74)
Уравнение (10) связывает между собой неизвестное значение функции ui,j с ее значениями в четырех соседних узлах. На сетке эти узлы образуют пятиточечный шаблон (рис. 6.5, а), позволяющий легко определить индексы в (6.74) для любого произвольно выбранного на сетке узла i,j .
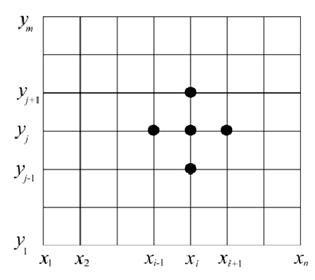
Рис. 6.5. Шаблон «крест» для уравнения эллиптического типа
Записывая (6.74)каждого узла 2<i<n‑1, 2<j<m‑1 и подставляя вместо i и j соответствующие номера, получимсистему связанных уравнений. Количетво уравнений будет равно количеству узлов, в которых необходимо найти неизвестные u i,i.Число неизвестных равно числу уравнений и система будет замкнутой.Значения функции u в узлах сетки, лежащих на границе рассматриваемой области, определяются заданными граничными условиями.
Решение системы алгебраических уравнений, получаемой в результате конечно-разностной аппроксимации уравнения эллиптического типа, является одним из наиболее тяжелых по вычислительным затратам этапов расчета. Для повышения точности решения приходится использовать сетки с большимчисломузлов, на которых формируются и довольно большие системы− нередко до нескольких тысяч алгебраических уравнений. Одним из способов уменьшения числа узлов иявляется использование сеток с неравномерным шагом. При этом сетку сгущают в наиболее важных с точки зрения точности участках, например, вблизи углов или отверстий.
В то же время решение задачи облегчается тем, что каждое из алгебраических уравнений содержит небольшое количество неизвестных. В качестве примера ниже приведена система с разреженной матрицей ленточного типа, полученной из (6.74) для прямоугольной области (рис. 6.5) при n = m = 5. В правой части записаны uij относящиеся к узлам, лежащим на границах.

Для решения подобных систем используют специальные методы, учитывающие разреженность матрицы коэффициентов. К специальным прямым относятся некоторые матричные методы и метод прогонки (аналог метода Гаусса). Из итерационных применяют метод Якоби (одновременных смещений) и метод Гаусса-Зейделя (последовательных смещений), а также модификации последнего, например, метод верхней релаксации.
Дата добавления: 2015-04-03; просмотров: 2193;
