Виробничо-транспортна задача
Розглянемо об’єкт економічної діяльності, який складається з виробничого блоку для забезпечення виробництва 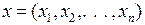 , де
, де 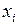 – кількість виробленої продукції і-го асортименту. Крім того, забезпечується доставка виробленої продукції до місця споживання (пунктів споживання). Пункти споживання можуть бути різні: склади, магазини, підрозділи, де продукція виступає як сировина, та ін. Усі вони є складовими частинами єдиної економічної системи (об’єкта економічної діяльності). Будемо вважати, що діяльність такої системи підпорядкована єдиній меті – максимізації прибутку:
– кількість виробленої продукції і-го асортименту. Крім того, забезпечується доставка виробленої продукції до місця споживання (пунктів споживання). Пункти споживання можуть бути різні: склади, магазини, підрозділи, де продукція виступає як сировина, та ін. Усі вони є складовими частинами єдиної економічної системи (об’єкта економічної діяльності). Будемо вважати, що діяльність такої системи підпорядкована єдиній меті – максимізації прибутку:
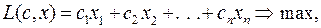 (15.1)
(15.1)
де 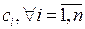 – вартість одиниці продукції і-го асортименту. Для простоти міркувань, розглядатимемо замкнену систему (без суттєвих зовнішніх впливів), що задовольняє умови рівноваги за В.В. Леонтьєвим [2]:
– вартість одиниці продукції і-го асортименту. Для простоти міркувань, розглядатимемо замкнену систему (без суттєвих зовнішніх впливів), що задовольняє умови рівноваги за В.В. Леонтьєвим [2]:
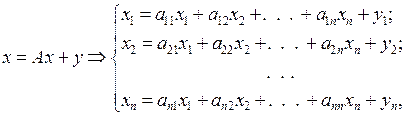 (15.2)
(15.2)
де 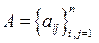 – технологічна (нормативна) матриця коефіцієнтів, а
– технологічна (нормативна) матриця коефіцієнтів, а 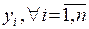 – кількість кінцевої продукції і-го асортименту; а також умови:
– кількість кінцевої продукції і-го асортименту; а також умови:
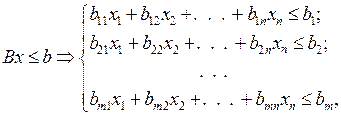 (15.3)
(15.3)
де 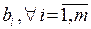 запаси ресурсів, що використовуються в процесі виробництва, m – їх кількість,
запаси ресурсів, що використовуються в процесі виробництва, m – їх кількість, 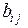 – нормативи використання j-го ресурсу для виробництва одиниці і-го продукту.
– нормативи використання j-го ресурсу для виробництва одиниці і-го продукту.
Транспортні витрати зменшують розмір прибутку, тому мають бути мінімальними. Суть досліджуваної проблеми полягає в гармонізації обсягу виробництва продукції з витратами на її транспортування для оптимізації прибутку так, щоб виконувалися умови (15.2), (15.3).
Для розв’язання даної задачі пропонується наступна схема. Будемо вважати, що всі величини задачі (15.1)-(15.3) мають вартісну сутність.
1. Розширимо матрицю А, додаючи до неї (n+1)-й стовпчик 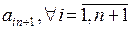 та (n+1)-й рядок
та (n+1)-й рядок 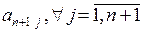 . Елементи матриці
. Елементи матриці 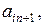
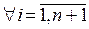 є технологічними коефіцієнтами витрат і-ї продукції для забезпечення одиничних перевезень (наприклад, перевезень вартістю в 1000 грн.). Елементи
є технологічними коефіцієнтами витрат і-ї продукції для забезпечення одиничних перевезень (наприклад, перевезень вартістю в 1000 грн.). Елементи 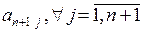 – розмір сумарних транспортних затрат для доставки одиниці j-ї продукції до місця призначення. Тоді система (15.2) має вигляд:
– розмір сумарних транспортних затрат для доставки одиниці j-ї продукції до місця призначення. Тоді система (15.2) має вигляд:
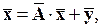 (15.4)
(15.4)
де 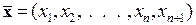 ,
, 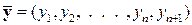 ;
; 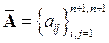 – роз-ширена та доповнена матриця сумарних транспортних затрат на перевезення всієї продукції системи;
– роз-ширена та доповнена матриця сумарних транспортних затрат на перевезення всієї продукції системи;
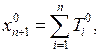
де 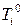 – сумарні транспортні затрати на перевезення продукції і-го асортименту. Покладемо
– сумарні транспортні затрати на перевезення продукції і-го асортименту. Покладемо 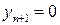 або будемо вважати, що затрат на власні перевезення немає.
або будемо вважати, що затрат на власні перевезення немає.
- Надалі опустимо знак «–» у формулі (15.4), і додамо знак «N». Тоді (15.4) можна переписати так:
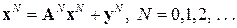
- Знаходимо обернену матрицю
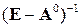 , де
, де
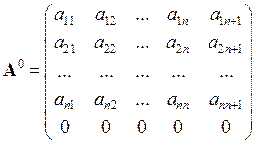
- Знаходимо
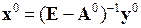
5. Підставляємо 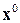 в (15.1) та (15.3) і зводимо подібні члени відносно
в (15.1) та (15.3) і зводимо подібні члени відносно 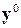 .
.
6. Розв’язуємо ЗЛП:
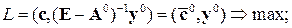
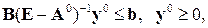
де 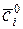 – компоненти вектора
– компоненти вектора 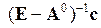 .
.
7. Знаходимо 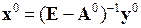 .
.
8. Формуємо ЗТТ:
| ППk ПВk | 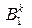
| 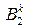
| … | 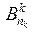
| |
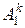
| 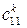
| 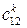
| … | 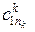
| 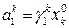
|
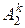
| 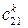
| 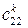
| … | 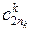
| 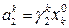
|
| … | … | … | … | … | … |
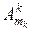
| 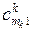
| 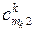
| … | 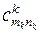
| 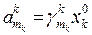
|
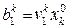
| 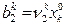
| … | 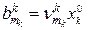
| 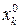
|
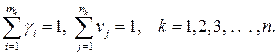
де 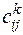 – вартості перевезень одиниці продукції з і-го пункту відправлення в
– вартості перевезень одиниці продукції з і-го пункту відправлення в
j-й пункт призначення для продукції k-го виду; 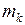 – кількість споживачів
– кількість споживачів
k-го виду продукції, 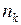 – кількість її виробників;
– кількість її виробників; 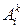 та
та 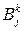 – відповідно пункти відправлення та призначення продукції k-го виду.
– відповідно пункти відправлення та призначення продукції k-го виду.
9. Обчислюємо 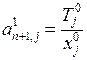 . Покладемо
. Покладемо 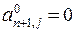 , одержаними числами
, одержаними числами 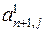 в матриці
в матриці 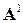 , де
, де 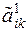 – елементи k-го стовпчика матриці повних затрат
– елементи k-го стовпчика матриці повних затрат 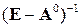 . В пп. 3-7 покладаємо замість знака «0» у змінних
. В пп. 3-7 покладаємо замість знака «0» у змінних 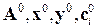 знак «1». Повторюємо виконання пп. 3-8, поступово нарощуючи на одиницю
знак «1». Повторюємо виконання пп. 3-8, поступово нарощуючи на одиницю 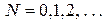 доти, доки виконується умова:
доти, доки виконується умова:
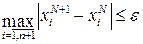
де 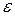 – наперед задане число, яке характеризує точність обчислень і задається ОПР;
– наперед задане число, яке характеризує точність обчислень і задається ОПР; 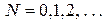
10. Розв’язком виробничо-транспортної задачі будуть 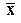 та
та 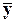 , які відповідно складають
, які відповідно складають 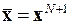 ,
, 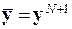 . Остання компонента вектора
. Остання компонента вектора 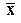 визначає сумарні оптимальні транспортні витрати економічного об’єкта.
визначає сумарні оптимальні транспортні витрати економічного об’єкта.
Завдання для самостійних і контрольних робіт
Розв’язати виробничо-транспортні задачі.
Транспортні таблиці мають такий вигляд:
І.
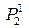
| 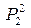
| С1 | С2 | М1 | М2 | ||
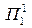
| 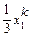
| ||||||
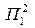
| 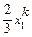
| ||||||
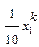
| 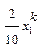
| 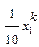
| 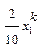
| 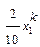
| 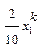
| 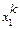
|
ІІ.
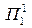
| 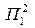
| С1 | С2 | М1 | М2 | ||
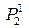
| 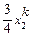
| ||||||
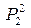
| 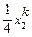
| ||||||
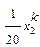
| 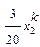
| 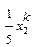
| 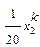
| 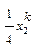
| 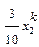
| 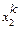
|
Примітка: 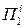 – підприємства, що випускають продукцію 1-го виду, і=1,2;
– підприємства, що випускають продукцію 1-го виду, і=1,2;
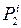 – підприємства, що випускають продукцію 2-го виду, і=1,2;
– підприємства, що випускають продукцію 2-го виду, і=1,2;
С1, С2 – склади; М1, М2 –магазини.
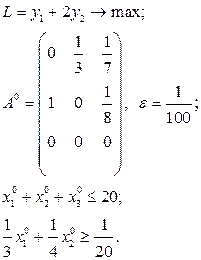
| 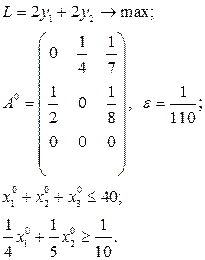
| ||
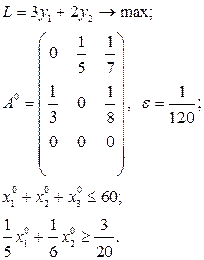
| 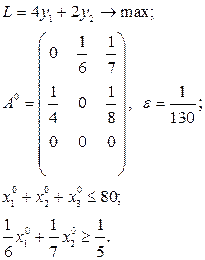
| ||
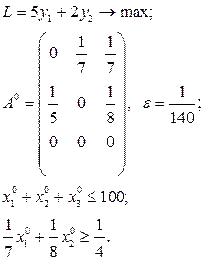
| 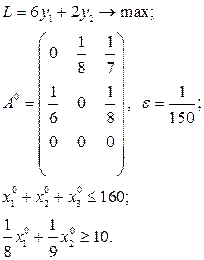
| ||
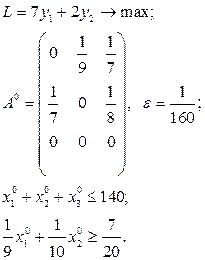
| 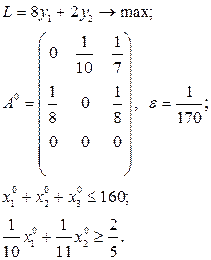
| ||
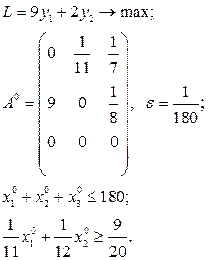
| 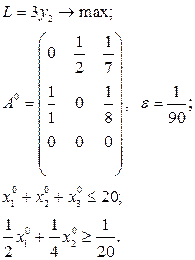
| ||
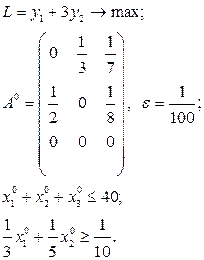
| 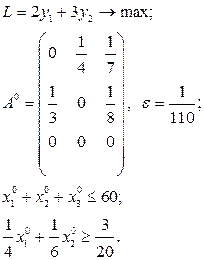
| ||
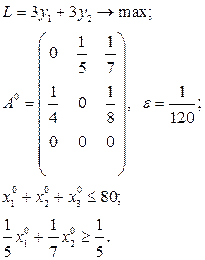
| 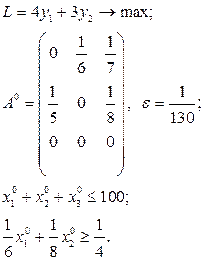
| ||
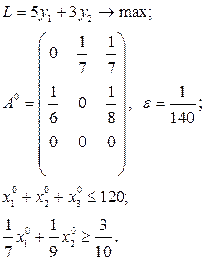
| 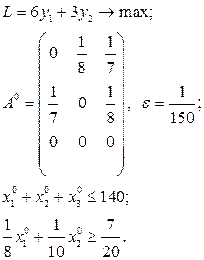
| ||
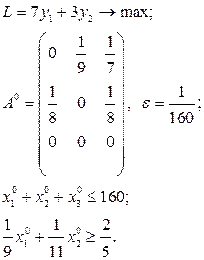
| 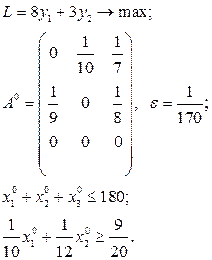
| ||
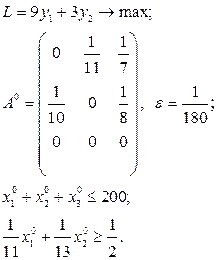
| 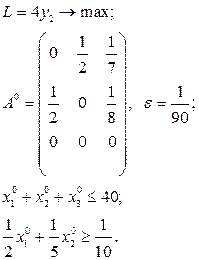
| ||
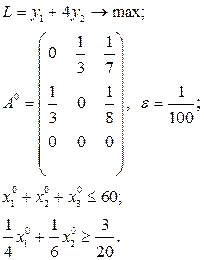
| 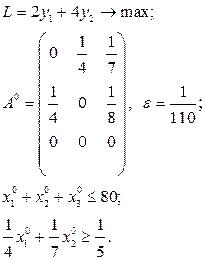
| ||
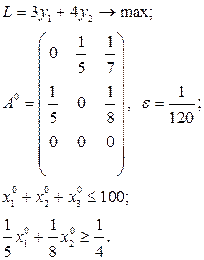
| 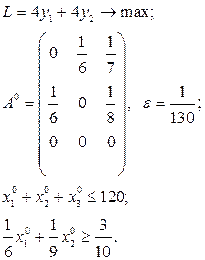
| ||
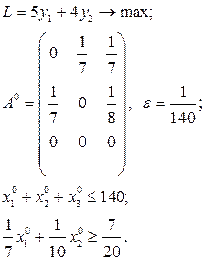
| 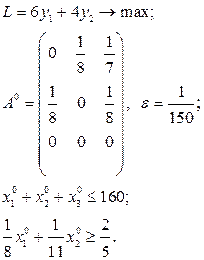
| ||
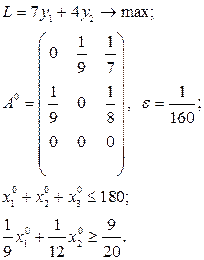
| 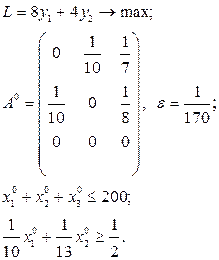
| ||
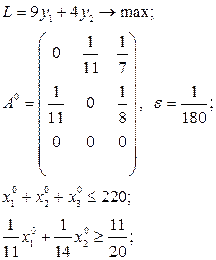
| 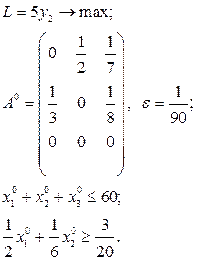
| ||
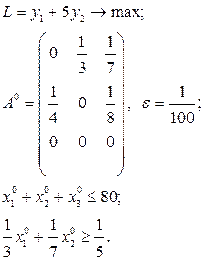
| 
|
Дата добавления: 2015-06-12; просмотров: 1637;
