Принцип максимуму Л. С. Понтрягіна
Розглянемо математичну модель оптимального керування. Нехай математична модель економічної системи має вигляд:
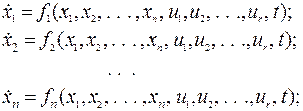 (16.1)
(16.1)
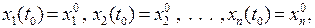
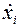 –похідна функції x(t) за t.
–похідна функції x(t) за t. 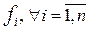 – неперервно-диференційовані функції за фазовими змінними
– неперервно-диференційовані функції за фазовими змінними 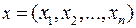 ;
; 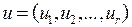 – вектор-параметр керування, який знаходиться в розпорядженні ОПР.
– вектор-параметр керування, який знаходиться в розпорядженні ОПР. 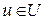 , де U – множина змінних вектор-параметра керування.
, де U – множина змінних вектор-параметра керування.
Будемо вважати, що треба перевести систему за фіксований час Т із стартового стану 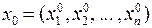 у такий стан
у такий стан 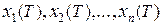 , у якому функціонал:
, у якому функціонал:
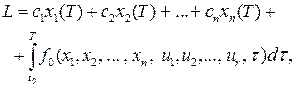 , (16.2)
, (16.2)
де 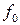 – диференційована функція аргументів
– диференційована функція аргументів 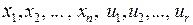 , досягає найменшого значення. Тобто, треба знайти таке оптимальне керування, набір
, досягає найменшого значення. Тобто, треба знайти таке оптимальне керування, набір 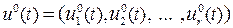 з множини U, і відповідну йому оптимальну траєкторію, що мінімізують функціонал (16.2).
з множини U, і відповідну йому оптимальну траєкторію, що мінімізують функціонал (16.2).
Спряженою до (16.1) будемо називати систему рівнянь:
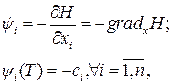 (16.3)
(16.3)
де H – функція Гамільтона:
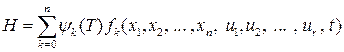 ,
, 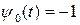 .
.
Сформулюємо теорему [4]: принцип максимуму Л. С. Понтрягіна.
Теорема.Для розв’язання задачі (16.1), (16.2) необхідне виконання умови:
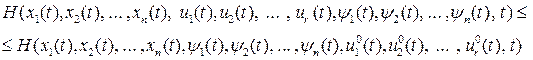 (16.4)
(16.4)
або
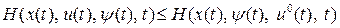
при кожному 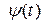 , що задовольняє (16.3).
, що задовольняє (16.3).
Очевидно, у разі виконання умови (16.4) на єдиному наборі 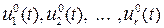 , та існування розв’язку задачі оптимального керування принцип максимуму є і достатньою умовою оптимальності
, та існування розв’язку задачі оптимального керування принцип максимуму є і достатньою умовою оптимальності 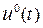 на розв’язках задачі (16.1), (16.3).
на розв’язках задачі (16.1), (16.3).
Проілюструємо застосування принципу максимуму на конкретному прикладі. Функції 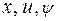 будемо вважати залежними від часу.
будемо вважати залежними від часу.
Приклад.Розв’язати макроекономічну задачу оптимального керування [7], якщо модель системи описується диференційним рівнянням вигляду:
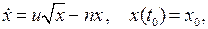 (16.5)
(16.5)
де х – відношення основного капіталу до кількості населення; u – частка національного доходу, спрямована на збільшення основного капіталу; n – амортизаційна постійна; 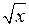 – виробнича функція.
– виробнича функція.
Математична модель (16.5) побудована на допущенні, що частка оплати праці дорівнює 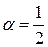 ;
; 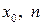 – задані числа,
– задані числа, 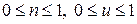 .
.
Задача полягає у знаходженні 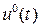 , що забезпечує мінімальне значення функціоналу:
, що забезпечує мінімальне значення функціоналу:
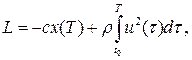 (16.6)
(16.6)
де 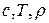 – наперед задані додатні числа.
– наперед задані додатні числа.
Алгоритм розв’язку задачі:
1. Будуємо функцію Гамільтона для задачі (16.5),(16.6):
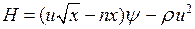 ,
,
де
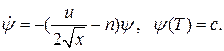 (16.7)
(16.7)
2. Згідно з принципом максимуму:
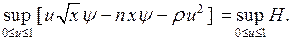
Спочатку не будемо зважати на нерівності 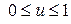 . Тоді:
. Тоді:
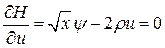 або
або 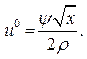 (16.8)
(16.8)
Підставимо отримане значення 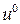 в (16.7).
в (16.7).
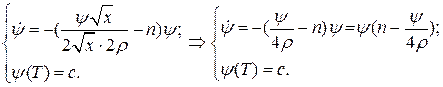 (16.9)
(16.9)
Отримаємо диференціальне рівняння з відокремлюваними змінними.
3. Розв’яжемо рівняння (16.9)
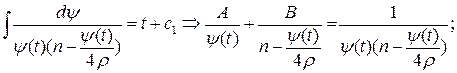
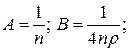
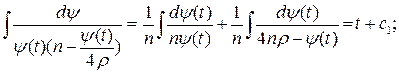
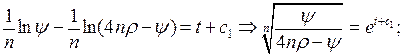
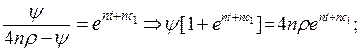
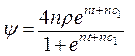
Враховуючи 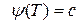 , отримаємо:
, отримаємо:
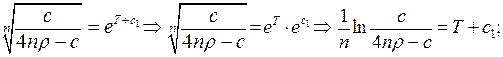
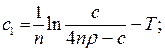
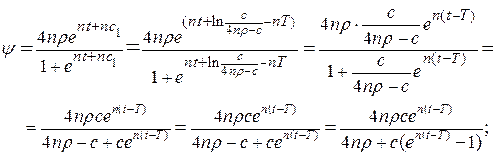
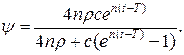
Оскільки знайдено 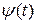 , для оптимального керування
, для оптимального керування 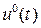 , що задовольняє принцип максимуму (16.4), то можна вважати
, що задовольняє принцип максимуму (16.4), то можна вважати 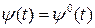 .
.
4. Знайдемо траєкторію 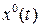 , для оптимального керування:
, для оптимального керування:
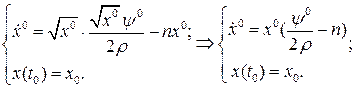
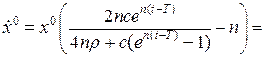
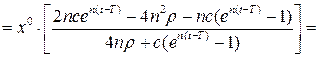
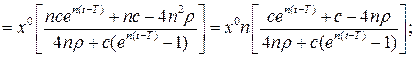
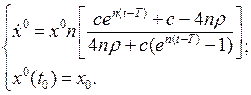
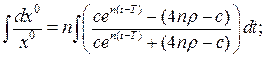
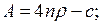
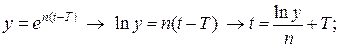
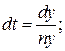
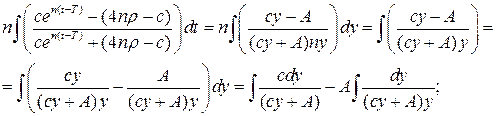
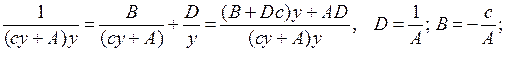
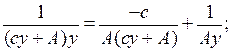
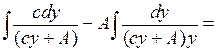
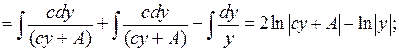
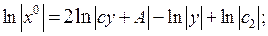
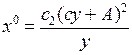 або
або 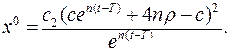
Враховуючи початкову умову 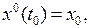
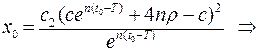
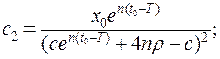
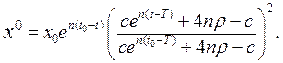
Підставляючи значення 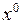 в (16.8) отримаємо
в (16.8) отримаємо
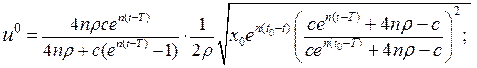
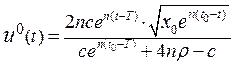
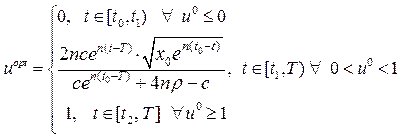
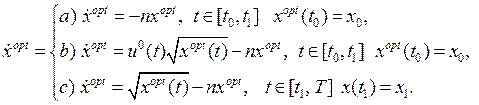
Знайдемо розв’язок для кожного з трьох випадків:
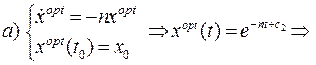
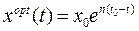
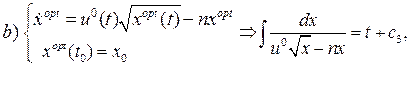
Проведемо заміну змінних: 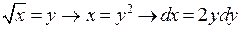
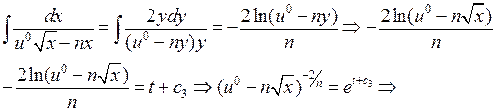
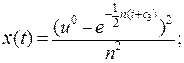
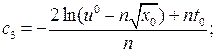
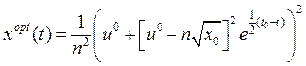
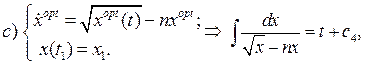
Як і в попередньому випадку покладемо: 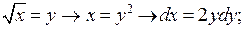
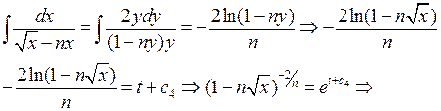
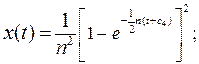
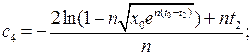
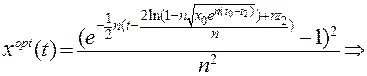
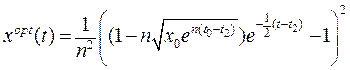
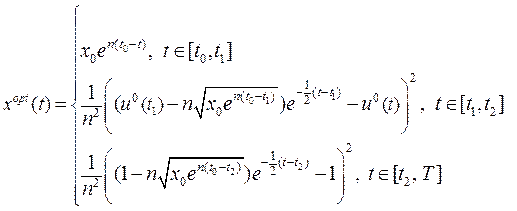 (16.19)
(16.19)
Завдання для самостійних і контрольних робіт
Розв’язати задачі оптимального керування.
| 1. | 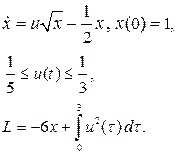
| 2. | 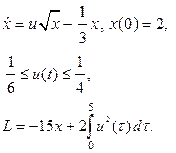
|
| 3. | 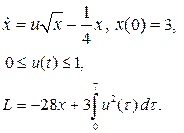
| 4. | 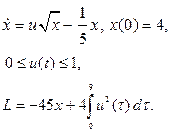
|
| 5. | 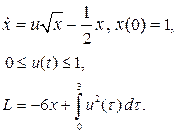
| 6. | 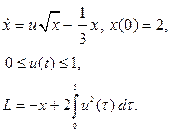
|
| 7. | 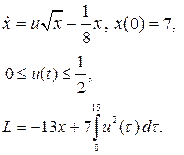
| 8. | 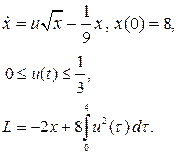
|
| 9. | 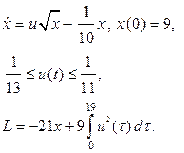
| 10. | 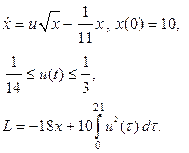
|
| 11. | 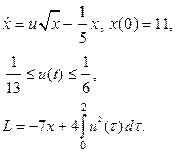
| 12. | 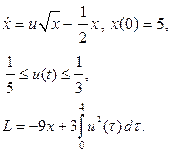
|
| 13. | 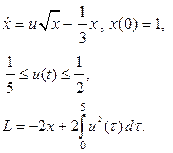
| 14. | 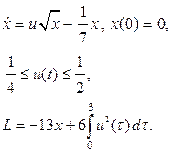
|
| 15. | 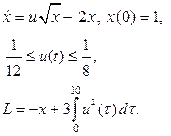
| 16. | 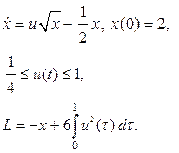
|
| 17. | 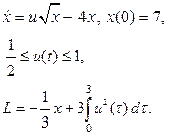
| 18. | 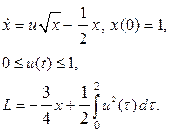
|
| 19. | 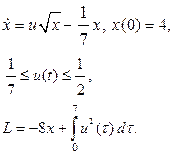
| 20. | 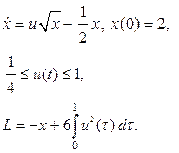
|
| 21. | 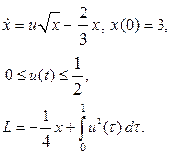
| 22. | 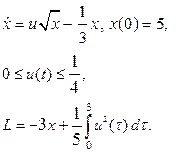
|
| 23. | 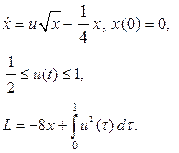
| 24. | 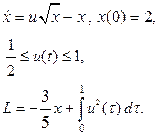
|
| 25. | 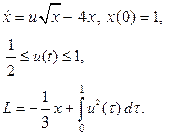
| 26. | 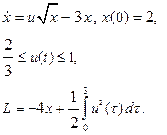
|
| 27. | 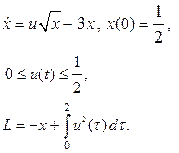
| 28. | 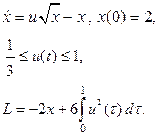
|
| 29. | 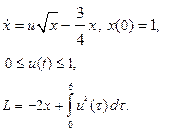
| 30. | 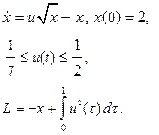
|
Дата добавления: 2015-06-12; просмотров: 1017;
