Выбор экономических факторов, построение модели.

1.1. Построение выборочных парных линейных регрессий результативного признака длякаждого из k = 3 факторов, , , …, .

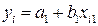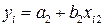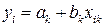Построение выборочных парных линейных регрессий выполняется для предварительного отбора наиболее существенных факторов, с помощью функции «ЛИНЕЙН», а также с помощью анализа данных (Данные - анализ данных – регрессия) (см. приложение 1. П. 1.1)

Регрессия y на x₁: y = 0,0353·x₁ + 22021, R² = 0,1012, 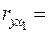0,3181, F = 8,44

Регрессия y на x₂ y = 0,21,171·x₂ + 172136, R² = 0,8786, 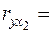0,93734, F=542.9

Регрессия y на x₃ у = 10.992х3 + 486405 R² = 0,71 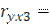0,8425, F = 183.5

В каждом случае выполнено построение поля корреляции, вычислены коэффициенты уравнения выборочной парной линейной регрессии, вычислены коэффициенты детерминации и корреляции, вычислены значеня 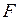статистики, проверка статистической значимости коэффициентов регрессии 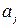, , 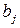и уравнения регрессии в целом;

Вывод. Частные парные регрессии показывают – что не все три фактора могут быть включены в модель множественной регрессии, т.к. коэффициент детерминации у одного из них меньше 0,3. (см. приложение 1, п.1.1)

1.2. Проверка мультиколлинеарности факторов.

Для дальнейшей работы с данными, нам нужно убедиться в том, что в модели отсутствует мультиколлинеарность.

Мультиколлинеарность — тесная корреляционная взаимосвязь между отбираемыми для анализа факторами x_i , совместно воздействующими на результирующий признак y, которая затрудняет оценивание регрессионных параметров и разделение влияния объясняющих факторов на поведение зависимой переменной.

Оценки параметров регрессии 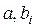и коэффициентов корреляции 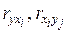оказываются нестабильными как в отношении статистической значимости, так и по величине и знаку (например, коэффициентов корреляции). Следовательно, они ненадежны. При этом значение коэффициента детерминации R² может быть высоким, свидетельствуя об адекватности модели.
Для проверки появления мультиколлинеарности вычисляются матрицы коэффициентов корреляции (частной) для всех объясняющих переменных. Если коэффициенты корреляции между отдельными объясняющими переменными велики 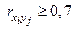, то они коллинеарны.

Признаком мультиколлинеарности может быть близость к нулю матрицы .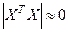

Однако не существует точных критериев, в соответствии с которыми можно установить наличие или отсутствие мультиколлинеарности отрицательно влияющей на качество выбранной модели регрессии. (см. приложение 1 п.1.2)

1.3. Построение матрицы Q выборочных коэффициентов корреляции.

Для выявления коррелированных факторных переменных с помощью функции КОРРЕЛЯЦИЯ Пакета Анализа составляется расширенная корреляционная матрицу .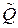

Расширенная матрица выборочных коэффициентов корреляции для результативного признака y и трех переменных 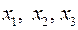имеет вид:

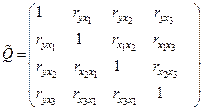
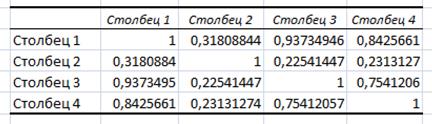
Матрица выборочных межфакторных коэффициентов корреляции имеет вид:

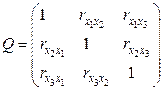
Вывод. После выполнения пунктов 1.1, 1.2, 1.3 можно сделать анализ результатов и предварительный отбор факторов для включения их в модели множественной регрессии. (см. приложение 1, п.1.3)

1.4. Вычисление коэффициентов выборочной множественной регрессии 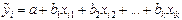. С помощью функции «ЛИНЕЙН» с двумя факторными переменными. (см. приложение 1, п.1.4)

Глава 2. Проверка качества модели.

2.1. Вычисление множественного коэффициента детерминации 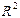и скорректированного (исправленного) коэффициента детерминации 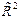, сделать вывод об адекватности модели.

Множественный коэф. Детерминации и скорректированный коэф. Детерминации имеют значения, близкие к единице, что говорит об адекватной модели. (см. приложение 1 п.2.1)

2.2. Вычисление остатков 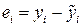и проверка гипотезы о нормальном законе распределения остатков. (см. приложение 1. П.2.2)

2.3. Вычисление средней ошибки аппроксимации 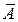. (в п.1.4)

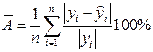
=0,26%

Ошибка аппроксимации имеет очень низкое значение, что говорит о хорошо подобранной модели уравнения. (см. приложение 1, п.2.3)

2.4. Проверка статистической значимости коэффициентов множественной регрессии и уравнения регрессии в целом пройдена. Все коэф. Регрессии статистически значимы (см. приложение 1, п.2.4)

2.5. Построение доверительных интервалов для статистически значимых коэффициентов регрессии.

Доверительные интервалы для параметров aи bс заданным уровнем доверия, в качестве которого на практике обычно выбирают вероятность 0,95 (соответствующую уровню значимости 0.05 или 5%).

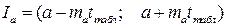
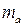– стандартная ошибка коэффициента регрессии ;

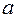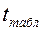– критическое значение для заданного уровня значимости и заданного числа степеней свободы n - 2.

;

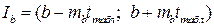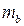– стандартная ошибка коэффициента регрессии .

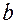2.6. Построение расширенной матрицы выборочных коэффициентов корреляции 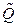. Вычисление частных коэффициентов корреляции между факторами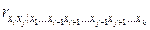

Вычисление выборочных коэффициентом частной корреляции между зависимой переменной yи объясняющей переменной x_j – .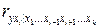

(Выполнено в п.1.3)

Вывод. На основании анализа пунктов 4 – 10 можно сделать выводы о том, что модель адекватна, но присутствовала мультиколлинеарность, вследствие чего пришлось выполнить отбор факторов исключением одного из них (с сильной межфакторной корреляционной зависимостью).

2.7. Пошагоый отбор наиболее существенных переменных в модели множественной линейной регрессии с использованием скорректированных коэффициентов детерминации 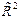и частных F- статистики.

Т.к. в исследовании осталось всего 2 факторных переменных, и в первую очередь была включена та, которая имеет наибольшую корреляцию с результирующим признаком, проводить отбор нецелесообразно, потому что. в любом случае, второй фактор, который в наименьшей степени влияет на результирующий, будет включён после включения первого. (см. приложение 1, п.2.7)

2.8. Проверка гипотезы о гомоскедастичности наблюдений по методу Голдфелда-Квандта и теста Спирмена.