Теоретические предпосылки.

Постоянство дисперсии случайных ошибок регрессионной модели независимо от наблюдения называетсягомоскедастичностью.

Гетероскедастичность свойство дисперсии случайных ошибок регрессионной модели противоположное гомоскедастичности.Гетероскедастичность означает неоднородность наблюдений, выражающуюся в неодинаковой (непостоянной) дисперсии случайной ошибки регрессионной (эконометрической) модели.

Гетероскедастичность существенно снижает качество оценок неизвестных параметров.

Теста Голдфелда-Квандта предполагает:

- возмущения 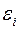являются нормально распределенными случайными величинами;

- отсутствует автокорреляция возмущений;

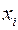- средние квадратические отклонения возмущений прямо пропорциональны значениям объясняющей переменной , что часто встречается на практике и означает постоянство относительного разброса возмущений (а не абсолютного, как предполагается в классической модели).

Тест состоит в следующем.

1. Все наблюдения упорядочиваются в порядке возрастания значения объясняющей переменной.

2. Полученная упорядоченная выборка разбивается на три части:

первая и последняя части содержат по lнаблюдений, средняя часть состоит из m = n - 2l

наблюдений.

Далее рассматриваются только две части: первая часть l наблюдений (с небольшими значениями объясняющей переменной) и третья часть lпоследних наблюдений (с большими значениями объясняющей переменной), а m центральных наблюдений исключаются из рассмотрения.

3. Оцениваются отдельные регрессии для первой ( l первых наблюдений) и второй ( l последних наблюдений) частей. В этом случае гипотеза гомоскедастичности равносильна тому, что значения остатков для первых и последних наблюдений представляют выборку значений нормально распределенных случайных величин, имеющих одинаковые дисперсии. Но, если верно предположение о пропорциональности дисперсий значениям объясняющей переменной (т.е. предположение о гетероскедастичности), то дисперсия (сумма квадратов остатков) для первой части будет существенно меньше дисперсии (суммы квадратов остатков) для второй части наблюдений.

4. Для сравнения дисперсий строится статистика

5. Если гипотеза гомоскедастичности верна, то F – статистика имеет распределение Фишера со степенями свободы . Для заданного уровня значимости по таблицам распределения Фишера-Снедекора определяется значение 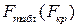как критическая точка, соответствующая степеням свободы (k – число факторов).

Тогда:

1. Если 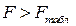, то гипотеза об отсутствии гетероскедастичности отклоняется;

2. Если 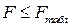, то гипотеза об отсутствии гетероскедастичности не отклоняется.

Для парной регрессии обычно предлагаются следующие размеры подвыборок:

для n = 30 значение l = 11;

для n = 60 значение l = 22 .

Тест Голдфелда-Квандта может использоваться и в случае предположения об обратной пропорциональности между дисперсией возмущений и значениями объясняющей переменной, при этом статистика F имеет вид

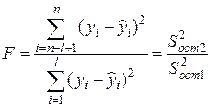
В случае множественной регрессии данный тест может проводиться для каждой объясняющей переменной по отдельности.

Проверка гипотезы о гомоскедастичности с помощью теста Спирмена.

Идея теста состоит в том, что в случае гетероскедастичности абсолютные величины остатков 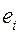(которые являются оценками возмущений) будут коррелировать со значениями объясняющей переменной .

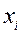Для проверки этого факта значения 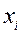и 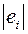, упорядочиваются по величине (ранжируются) и для каждого значения определяется ранг — его номер в ранжированном ряде. Далее находится коэффициент ранговой корреляции .

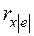Вычислите коэффициент ранговой корреляции Спирмена по формуле

,

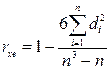где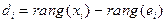

Проверьте статистическую значимость коэффициента ранговой корреляции с помощью выборочной статистики

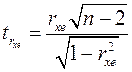
Статистика 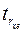распределена по закону Стьюдента с n – 2 степенями свободы.

Для выбранного уровня значимости a = 0,05 по таблице распределения

Стьюдента с n – 2 степенями свободы определяется 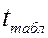, как критическая точка, соответствующая двусторонней критической области.

Тогда:

1) Если 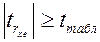, то гипотезу о равенстве нулю коэффициента

ранговой корреляции отклоняется, коэффициент корреляции статистически значим и, следовательно, отклоняется гипотеза об отсутствии гетероскедастичности, наблюдения гетероскедастичны;

2) Если 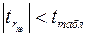, то гипотеза об отсутствии гетероскедастичности не отклоняется, коэффициент корреляции статистически незначимо отличается от нуля, наблюдения гомоскедастичны.

Если в модели несколько объясняющих переменных, то проверка гипотезы может осуществляться для каждой из них по отдельности.

(см. приложение 1, п.2.8)