Интегрирование ОДУ первого порядка в полярных дифференциалах. Интегрирующий множитель.
Интегрирование ОДУ первого порядка в полных дифференциалах. Интегрирующий множитель.
Дано уравнение вида 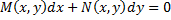
Если левая часть есть дифференциал некоторой функции u(x,y): 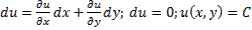 – общий интеграл уравнения; если
– общий интеграл уравнения; если 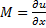 , а
, а 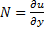 , то критерий полного дифференциала
, то критерий полного дифференциала 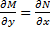 .
.
Предположим, что критерий выполняется. Найдём эту функцию u. Пусть 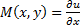 , тогда
, тогда 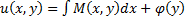 . Так как
. Так как 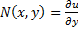 , то
, то 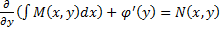 . Отсюда находится φ'(y).
. Отсюда находится φ'(y).
Пример: 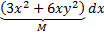 +
+ 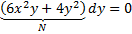
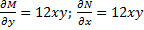
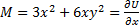
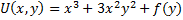
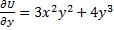
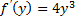
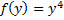
Интегрирующий множитель.
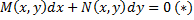 – неполный дифференциал.
– неполный дифференциал.
Существует ли функция 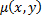 (интегрирующий множитель) по умножению на которую (*) станет полным дифференциалом?
(интегрирующий множитель) по умножению на которую (*) станет полным дифференциалом?
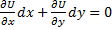
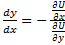
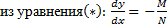
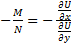
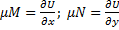
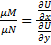
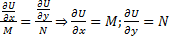
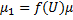
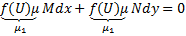
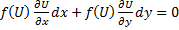
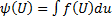
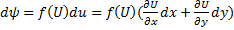
Если найдены два интегрирующих множителя 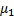 и
и 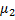 , то
, то 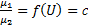 – решение.
– решение.
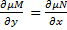
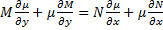
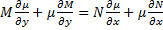
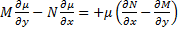
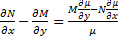
Если 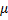 зависит только от x
зависит только от x 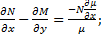
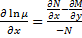
Пример: 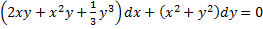
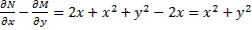
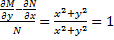
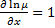
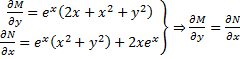
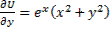 ;
; 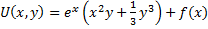
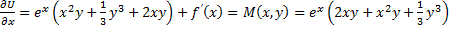
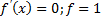
Интегрирующие комбинации:
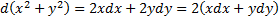
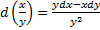
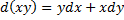
Дата добавления: 2015-05-16; просмотров: 1212;
