Оператор Гамильтона. (набла) его применение (примеры).

Оператор набла (оператор Гамильтона) – векторный дифференциальный оператор, обозначаемый символом 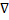. Для трёхмерного евклидова пространства в прямоугольных декартовых координатах оператор набла определяется следующим образом: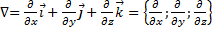

Для трёхмерного евклидова пространства в прямоугольных декартовых координатах. оператор набла определяется следующим образом:

,

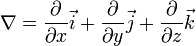где 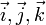— единичные векторы по осям x, y, z.

Через оператор набла естественным способом выражаются основные операции векторного анализа: grad (градиент), div (дивергенция), rot (ротор), а также оператор Лапласа (см. ниже). Широко употребляется в описанном смысле в физике и математике (хотя иногда графический символ используется также для обозначения некоторых других, хотя в некотором отношении не совсем далеких от рассмотренного, математических объектов, например, ковариантной производной).

Под n-мерным оператором набла подразумевается вектор с компонентами 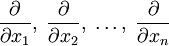в n-мерном пространстве.

36. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (ОДУ) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.

Дифференциальным уравнением называется соотношение 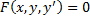, в котором x – независимая переменная, y – искомая функция. Это обыкновенное дифференциальное уравнение (ОДУ) первого порядка.

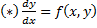– уравнение, разрешённое относительно производной.

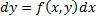
f(x,y) – заданная, непрерывная в некоторой области D переменных (x,y) функция.

Пусть 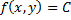. График функции 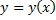называется интегральной кривой, 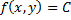– изоклины кривые.

Пусть правая часть уравнения (*) не зависит от y, то есть 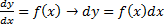, тогда .

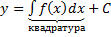На рисунке представлено семейство интегральных кривых, зависящих от одного параметра C.

Пусть 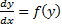. Будем считать независимой переменной y, а x – функция от y, то есть 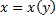. Тогда 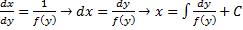. Но если 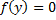и это уравнение имеет корень 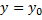, то добавляется решение, которое надо добавить к общему семейству, зависящему от параметра C.

Всякая функция вида 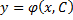при подстановке в (*), после чего (*) становится тождеством, является решением (общим решением дифференциального уравнения (*)).

Если C взято равным конкретному числу, то решение φ(x,C0) называется частным решением уравнения (*). 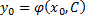- отсюда находится значение C.

Условие Коши – когда указано, какому x0 соответствует y0. Задача Коши: 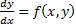– условие уравнения + условие Коши, то есть 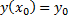. Задачу Коши геометрически можно сформулировать так: среди всех интегральных кривых уравнения (*) найти ту кривую (рисунок слева), которая проходит через заданную точку (x0, y0).

Пример. Дано: 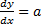и 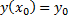. Решить задачу Коши.

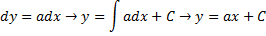
Когда 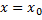, то :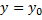

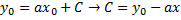
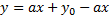
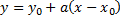– частное решение задачи Коши.