Вычисление разности потенциалов по напряженности поля.

Установленная связь между напряженностью поля и потенциалом позво­ляет по известной напряженности поля найти разность потенциалов между двумя произвольными точками этого поля.

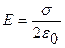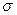1. Поле равномерно заряженной бесконечной плоскости определяется формулой , где - поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях х₁ и х₂ от плоскости (используем формулу (1.22)), равна

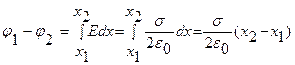
2. Поле двух бесконечных параллельных разноименно заряженных плоскостей определяется формулой 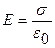. Разность потенциалов между плоскостями, расстояние между которыми равно d, равна

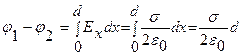. (1.9.1)

3. Поле равномерно заряженной сферической плоскости радиуса R с общим зарядом Q вне сферы (r > R) вычисляется по формуле .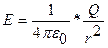

Разность потенциалов между двумя точками, лежащими на r₁ и r₂ от центра сферы (r₁ > R, r₂ > R), равна

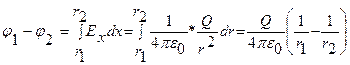. (1.9.2)

Если принять r₁ = r и r₂ = , то потенциал пола вне сферической поверхности задается выражением 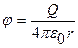. График зависимости 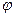от r приведен на рис.1.9.1

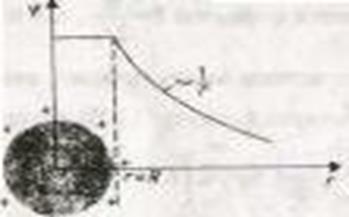
Рис.1.9.1

4. Поле равномерно заряженного цилиндра радиуса R, заряженного с линейной плотностью 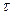, вне цилиндра (r > R) определяется формулой 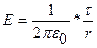. Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от оси заряженного цилиндра (r₁>R, r₂ >R), равна

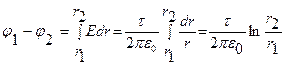(1.9.3)