Циркуляция вектора напряженности электростатического поля.

Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории (рис.1.6.1) перемещается другой точечный заряд Q₀, то сила, приложенная к заряду, совершает работу. Работа силы 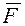на элементарном перемещении равна

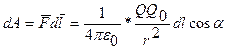
Так как 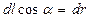, то

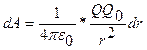
Работа при перемещении заряда Q из точки 1 в точку 2

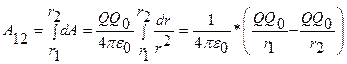(1.6.1)

не зависит от траектории перемещения, определяется только положениями начальной 1 и конечной 2 точек.

Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.

Рис.1.6.1

Из формулы (1.12) следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.

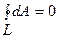(1.6.2)

Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительны и заряд, то элементарная работа сил поля на пути равна , где Е₁=Е соs 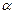- проекция вектора 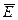на направление элементарного перемещения. Тогда формулу (1.6.2) можно записать в виде

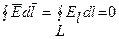(1.6.3)

Интеграл 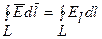называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее свойством (1.6.3), называется потенциальным. Из обращения в нуль циркуляция вектора 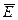следует, что линии напряженности электростатического поля не могут быть замкнутыми,они начинаются и кончаются на зарядах (соответственно на положительных и отрицательных) или же уходят в бесконечность.