Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.
 Рассмотрим кусок поверхности S, заданной уравнением F=(x,y,z)=0. Пусть выполняется условие
Рассмотрим кусок поверхности S, заданной уравнением F=(x,y,z)=0. Пусть выполняется условие 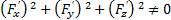 , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором
, что означает, что в каждой точке поверхности существует нормаль с направляющим вектором 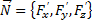 . Разобьем поверхность S сеткой гладких кривых на элементарные области
. Разобьем поверхность S сеткой гладких кривых на элементарные области 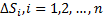 (разбиение Z). Пусть
(разбиение Z). Пусть 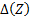 – наибольший из диаметров элементарных областей. Если независимо от разбиения Z существует
– наибольший из диаметров элементарных областей. Если независимо от разбиения Z существует 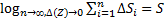 , то он и называется площадью данной поверхности. Пусть S однозначно проектируется на плоскость xy и G – это проекция. Элементу площади dxdy области G на плоскости xy соответствует элемент площади поверхности S, равный
, то он и называется площадью данной поверхности. Пусть S однозначно проектируется на плоскость xy и G – это проекция. Элементу площади dxdy области G на плоскости xy соответствует элемент площади поверхности S, равный 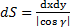 , где
, где 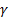 – угол между нормалью к поверхности S и осью Z. Поэтому вычисление площади поверхности сводится к вычислению двойного интеграла
– угол между нормалью к поверхности S и осью Z. Поэтому вычисление площади поверхности сводится к вычислению двойного интеграла  по проекции поверхности на плоскость. Если поверхность задана уравнением
по проекции поверхности на плоскость. Если поверхность задана уравнением 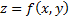 ,
, 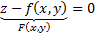 , а нормаль представляет собой градиент функции, то есть:
, а нормаль представляет собой градиент функции, то есть: 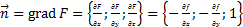 , то
, то 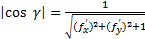 и площадь поверхности вычисляется по формуле:
и площадь поверхности вычисляется по формуле:
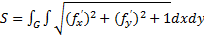 , здесь G – проекция поверхности S на плоскость xy.
, здесь G – проекция поверхности S на плоскость xy.
Если поверхность однозначно проектируется на другие координатные плоскости, то соответственно изменится формула вычисления площади поверхности.
Если кривая задана параметрическими уравнениями 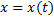 и
и 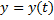 , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми
, то площадь криволинейной трапеции, ограниченной этой кривой, прямыми 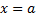 и
и 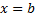 и отрезком [a,b] оси Ox, выражается формулой
и отрезком [a,b] оси Ox, выражается формулой 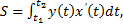 где
где 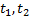 определяются из уравнений
определяются из уравнений 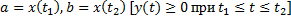
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением 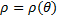 и двумя полярными радиусами
и двумя полярными радиусами 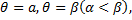 находится по формуле
находится по формуле
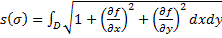 .
.
Дата добавления: 2015-05-16; просмотров: 3592;
