Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.
Замена переменных в тройном интеграле в общем случае.
 Пусть имеется тело (V) с границей (S).
Пусть имеется тело (V) с границей (S). 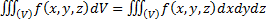
Пусть 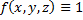 , тогда
, тогда 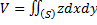 .
.
Замена: 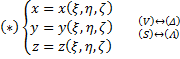
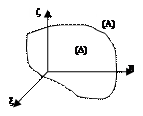 Преобразование (*) будем считать взаимно-однозначным, то есть всё можно выразить друг через друга, а именно:
Преобразование (*) будем считать взаимно-однозначным, то есть всё можно выразить друг через друга, а именно: 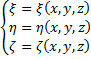
Пусть поверхность (Λ) задаётся параметрически, то есть: 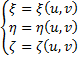
Получаем параметрическое задание поверхности (S) (см. рис. ниже).

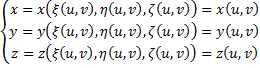
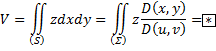
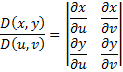
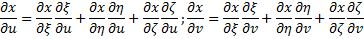
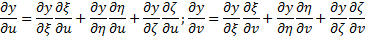
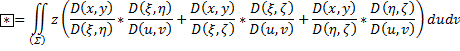
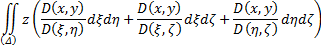
Два последних двойных интеграла равны, так как: 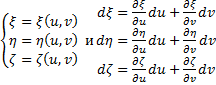
Применим к последнему выражению формулу Гаусса-Остроградского, то есть эту формулу: 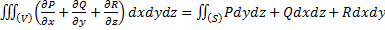 .
.
Пусть 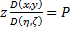 ,
, 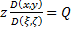 ,
, 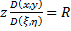 , тогда:
, тогда:
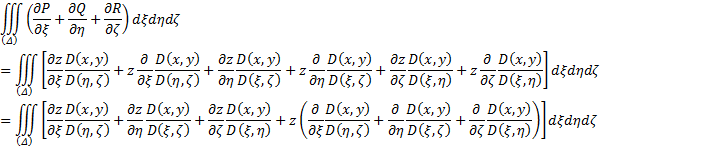
Выражение в скобках равно нулю. Оставшееся выражение запишем так:
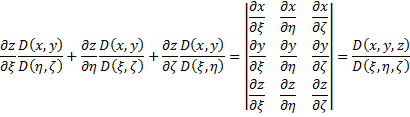
Это якобиан преобразования. Окончательно получаем: 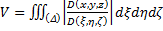
А для общего случая:
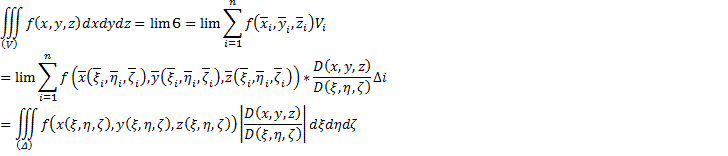
 Цилиндрические координаты:
Цилиндрические координаты:
Переходим от координаты M(x,y,z) к M(ρ,φ,z). Это цилиндрические координаты, где: 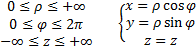
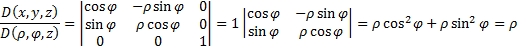
Получаем, что 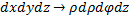 .
.
 Сферические координаты:
Сферические координаты:
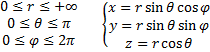
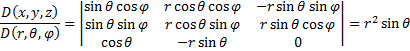
Получаем элемент объёма сферических координат: 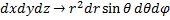 .
.
Дата добавления: 2015-05-16; просмотров: 1372;
