Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.
Производные ФНП.
Рассмотрим функцию u = F(x), определенную в некоторой области D. Пусть 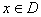 − фиксированная точка. Дадим координате х1 приращение
− фиксированная точка. Дадим координате х1 приращение  . Если существует конечный предел
. Если существует конечный предел 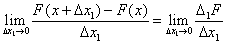 , то он называется частной производной функции F(x) по переменной х1 и обозначается
, то он называется частной производной функции F(x) по переменной х1 и обозначается 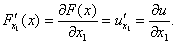
Аналогично определяются частные производные по всем остальным переменным.
Замечания.
1. Частная производная по какой либо переменной есть обычная производная, при условии, что все остальные переменные – константы.
2. Последнее обозначение, в отличие от функций одной переменной, не равно частному от деления двух дифференциалов, а является неразрывным символом.
В частном случае двух переменных частная производная равна тангенсу наклона касательной к сечению поверхности плоскостью, перпендикулярной ко второй переменной.
Примеры.
Частные производные высших порядков.
Вычисляя частные производные ФНП, мы снова получаем функцию тех же переменных, от которой можно взять частную производную, в том числе и по другой переменной (если она, конечно, существует): 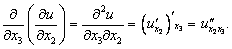 Частные производные по одной и той же переменной называются повторными, а по различным переменным – смешанными. Например:
Частные производные по одной и той же переменной называются повторными, а по различным переменным – смешанными. Например: 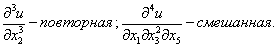
Примеры.
Теорема 1 (О равенстве смешанных производных). Пусть функция z = f(x,y) имеет вторые частные производные в окрестности т. М0 , непрерывные в самой точке М0.
В этом случае 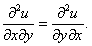
{Рассмотрим функции 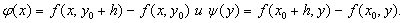
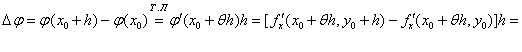
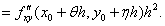 Для
Для 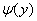 аналогично получаем:
аналогично получаем: 
Из равенства  следует
следует
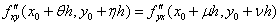 . Устремив h к нулю , в силу непрерывности производных, получаем:
. Устремив h к нулю , в силу непрерывности производных, получаем:  }
}
Если u = u(x1,…,xn), то все вторые частные производные можно записать с помощью
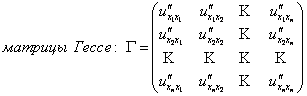 .
.
Из т.1 следует, что матрица Гессе – симметрична.
Дифференциал ФНП.
Пусть функция u = F(x) определена в области D и 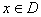 − фиксированная точка. Дадим приращение каждому аргументу хţ :
− фиксированная точка. Дадим приращение каждому аргументу хţ : 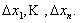 Величину
Величину 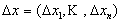 будем называть вектором приращения. В свою очередь функция u получит приращение равное
будем называть вектором приращения. В свою очередь функция u получит приращение равное
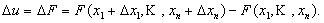
Определение 1. Функция u = F(x) называется дифференцируемой в т. х , если ее приращение может быть представлено в следующем виде:
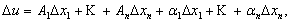 где
где
Aţ = Aţ(x) и не зависит от Δх, а 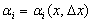 − бесконечно малая при
− бесконечно малая при 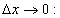
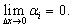
Величина вектора Δх равна: 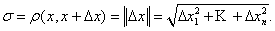
Используя это обозначение, можно написать 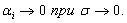
Легко показать, что 
{ 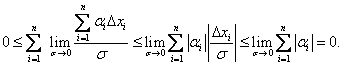 }
}
Определение 2. Главная и линейная часть приращения дифференцируемой функции называется дифференциалом: 
Теорема 1. Функция, дифференцируемая в т. хo − непрерывна в этой точке. { 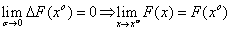 }
}
Теорема 2. (Необходимое условие дифференцируемости) Если F(x) дифференцируема в т. х , то она имеет все частные производные в этой точке, причем 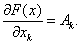
{Пусть 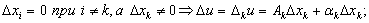
 }
}
Отсюда, 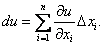 Если х − независимая переменная, то
Если х − независимая переменная, то 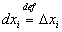 и окончательно
и окончательно

Теорема 3. (Достаточное условие дифференцируемости) Пусть F(x) имеет все частные производные в окрестности т. хо , непрерывные в самой этой точке. Тогда функция дифференцируема в т. хо .
{без доказательства}
Замечание. Для дифференцируемости функции одной переменной достаточно существования производной.
Дифференциал функции u называют полным дифференциалом.
Определение 3. Выражение 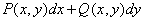 называется дифференциальной формой.
называется дифференциальной формой.
Теорема 4. Дифференциальная форма является полным дифференциалом некоторой функции u(х,у) тогда и только тогда, когда выполнено условие 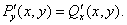
{1.Необх.: 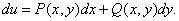 Тогда
Тогда 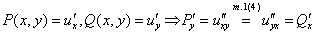
2. Дост. – без доказательства}
Пример. Найти общее решение дифференциального уравнения:
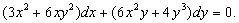
Геометрический смысл дифференцируемости. Касательная плоскость и нормаль к поверхности.
Рассмотрим поверхность S: z = f(x,y), дифференцируемую в т. 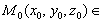 S.
S.
Определение 1. Плоскость, проходящая через т. М0 , называется касательной плоскостью к поверхности S в т.М0 , если угол между ней и секущей (М0М1) ( 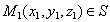 ) стремится к нулю при
) стремится к нулю при 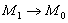 .
.
Определение 2. Вектор, ортогональный к касательной плоскости в т.М0 , называется нормальным вектором к поверхности в этой точке. Нормалью к поверхности называется
прямая, проходящая через т.М0 перпендикулярно касательной плоскости в этой точке.
Обозначим 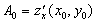 ,
, 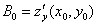 . Вектор приращения:
. Вектор приращения: 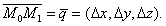
Из условия дифференцируемости функции z следует, что 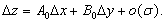
Рассмотрим плоскость 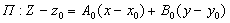 и угол φ между секущей и этой плоскостью:
и угол φ между секущей и этой плоскостью: 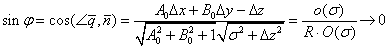 при
при  Отсюда сразу следует, что плоскость П – касательная к поверхности в т.М0. В результате имеем:
Отсюда сразу следует, что плоскость П – касательная к поверхности в т.М0. В результате имеем:
Функция z = f(x,y), дифференцируемая в некоторой точке (х0,у0) имеет в соответствующей т.М0 касательную плоскость: 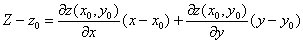 и нормальный вектор
и нормальный вектор 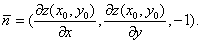
Пример. 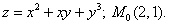
Дифференциалы высших порядков.
Определение 1. Дифференциал от первого дифференциала функции называется вторым дифференциалом: 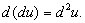 Аналогично определяются дифференциалы более старших порядков.
Аналогично определяются дифференциалы более старших порядков.
Вычислим второй дифференциал функции двух переменных 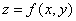 . При этом будем считать, что дифференциалы независимых переменных dx и dy – величины постоянные (т.е. не зависят от т.(х,у) и не меняются при вычислении каждого последующего дифференциала).
. При этом будем считать, что дифференциалы независимых переменных dx и dy – величины постоянные (т.е. не зависят от т.(х,у) и не меняются при вычислении каждого последующего дифференциала).
 .
.
Не трудно видеть, что второй дифференциал представляет собой квадратичную форму от
переменных dx и dy. Матрица этой квадратичной формы есть матрица Гессе, т.е.
d2z = (dx,dy)Г(dx,dy)T (см. раздел «Линейная алгебра», квадратичные формы). Кроме того,
второй дифференциал можно записать в символическом виде: 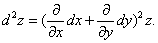
Можно показать, что в общем случае дифференциал 2 – го порядка функции u = F(x) равен 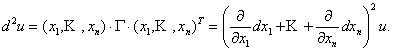
Дифференциал m – го порядка равен 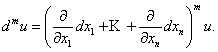
Дата добавления: 2015-05-16; просмотров: 1686;
