Степенной ряд. Теорема Абеля.

Важным случаем функциональных рядов являются степенные ряды:

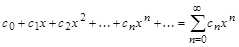(13)

или

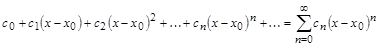
Для выяснения свойств степенных рядов достаточно ограничиться рассмотрением рядов вида (13), так как ряд по степеням 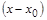легко свести к виду (13) заменой переменных 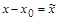, т.е. переносом начала координат в точку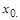

Для выяснения характера области сходимости степенного ряда сформулируем следующую теорему:

Теорема 6.1. (Абеля):

Пусть степенной ряд (13) сходится в точке 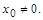Тогда он сходится абсолютно в любой точке х, для которой 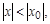и равномерно в любой области .

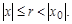Если степенной ряд (13) расходится в точке 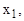то он расходится и во всех точках 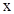таких, что .

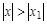Для определения области сходимости степенного ряда используется либо признак Даламбера, либо признак Коши.

Рассмотрим степенной ряд:

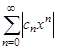. (14)

Вычислим предел:

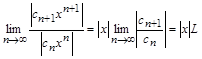.(15)

Если существует предел (15), то ряд (14) сходится, если 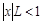, и расходится, если 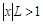. Следовательно, ряд (14) сходится абсолютно, если

,

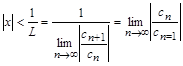и расходится, если

.

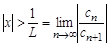Определение:

Число 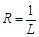, такое, что для всех x, удовлетворяющих условию 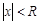ряд (13) сходится, а для всех х удовлетворяющих условию 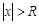ряд расходится, называется радиусом сходимости ряда.

Формула для радиуса сходимости, получаемая с помощью признака Даламбера, имеет вид

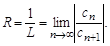(16)

Область сходимости ряда - так называют множество точек сходимости функционального ряда, т.е. множество значений аргумента х, для которых ряд (бесконечная сумма)
сходится

Пример 6.1.

Найти область сходимости ряда Область сходимости ряда

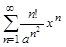при .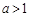

По признаку Даламбера:

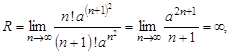
что означает, что ряд сходится на всей оси Х.